Paper halving
A thinking mathematically targeted teaching resource, focused on building understanding of halves using paper folding and visualising.
Syllabus
Syllabus outcomes and content descriptors from Mathematics K–10 Syllabus (2022) © NSW Education Standards Authority (NESA) for and on behalf of the Crown in right of the State of New South Wales, 2024.
Outcomes
- MAO-WM-01
- MAE-GM-03
- MAE-2DS-01
- MAE-2DS-02
- MAO-WM-01
- MA1-GM-03
- MA1-2DS-02
- MA1-2DS-01
Collect resources
You will need:
- a few sheets of A4 paper
- scissors
- coloured markers or pencils.
Paper halving – part 1
Watch Paper halving – part 1 video (11:58).
[Bold, white text on a dark blue background: Paper halving – part 1. From NRICH. In the bottom right corner is the red waratah logo of the NSW Government. In the bottom left corner is the text NSW Mathematics Strategy Professional Learning team (NSWMS PL team)]
Speaker
Hi there, mathematicians. We hope you're having a really lovely day today. We're here for a fantastic investigation called paper halving, and this comes from NRICH Maths.
[New slide: You will need…
- Sheets of A4 Paper
- Scissors
- Coloured markers/pencils
To the right of the text is an image of 4 sheets of A4 Paper, a pair of scissors and a row of variously coloured markers.
In the top right corner is small font is the text: NSW Department of Education.]
For today's investigation, you're going to need some sheets of A4 paper, some scissors, and some coloured markers or pencils.
[New slide: What do you notice?...]
Alright, let's get ready. What do you notice?
[New slide: The screen is divided into a cross-section.]
So, I'm gonna show you some images and I'd like you to write down or to draw a picture of what you notice. Eyeballs ready?
[In the top-left section an image appears of a tray of 12 muffins, organised in 4 columns and 3 rows. The left six muffins are decorated with pink icing, while the right six muffins are undecorated.]
What do you notice? Pause the video and write down or draw what you notice. When you're ready, press play again. Ah, yes. Some of you are saying that it looks like we've got a collection of cupcakes or muffins. Yes. And some of you are noticing that the muffins are arranged in an array.
[A red outline appears around the tray of muffins. Green outlines then appear around each row of four muffins. Each row has two pink muffins and two undecorated muffins.]
Do you see that? Yeah, because we've got even rows and columns. There's one row of four, two rows of four, and three rows of four, yeah. Ah, yes. And we could use that to help figure out how many there are altogether, couldn't we? Yeah. Because we know that double four is eight, and then four more, yeah, is 12.
[The coloured outlines disappear.]
And some of you are saying that we could also look at these muffins as two different types of muffins.
[An orange-line appears around the 6 pink-iced muffins and a blue line appears around the 6 undecorated muffins.]
And when we look at that, we can see that there are two smaller arrays within the larger array. Yeah.
[Yellow outlines appear around the rows in the pink-iced array and blue outlines around the undecorated muffins.]
And each of these arrays has one row of two, two rows of two, three rows of two. And the same for the blueberry. Yeah. And we can use this to help us quantify or figure out how many there are. So, we can skip count by twos, can't we? There are two, four, six muffins with pink icing and two, four, six muffins with blueberries in them. Yum. OK, I'm going to show you another image and your job is to write down or draw what you notice. Eyeballs ready?
[An image of a string of beads appears in the bottom left section. There are 5 pink beads above 5 green beads]
What do you notice this time? Pause the video now and press play when you're ready to continue. Yes. Yes. Some of you are seeing that we've got another collection, but this time a collection of beads.
[A red outline appears around the beads.]
Yes. And some of you are saying that there are two different coloured beads in this collection. Yes. And you can see that there are actually five green beads. And I can do that because of my subitising skills. Our brain has this amazing way of being able to really quickly quantify small collections.
[The area around the bottom 3 green beads is outlined and shaded in green. Then the other 2 green beads are outlined and shaded in green.]
So, I can see here that there are three and two more green beads, which I know is five.
[A pink outline and shade appears around the bottom 3 and then then 2 top pink beads.]
And then here there are three and two more pink beads, so five again. And I know that double five is ten. So, we have a total of ten beads. So, my next question to you, mathematicians, is what do you notice that is the same between these two images? Yes. Yes. Some of you are saying that they are both showing collections of objects. Yes. And they're both showing two different types of those objects, aren't they? Yeah. We've got the pink icing muffins and the blueberry muffins and then the pink beads and the green beads.
[The image of the beads is turned horizontally, so that the pink beads are on the left of the green beads.]
And maybe if we turned our image this way, that would be even easier to see. Yeah. We have pink beads and pink icing on one side and green beads and blueberry muffins on the other side.
[All of the added outlines are removed and the bead image is turned back to its original, vertical position.
OK, I'm going to show you another image. And what do you notice, and what's the same? Ready?
[In the bottom right section there is an image of an orange cut in half.]
Pause the video so you can write or draw your thinking. And then press play. Yes. Some of you are saying that you noticed that it's an orange, and it looks delicious, doesn't it? Yes. And this time we've just got one object, don't we? One whole orange. Yeah, not a collection of objects like the other images. Ah, but yes, it does. It looks like this orange has been sliced so that it's in two pieces, two parts. Yes, and they both look like they're the same size, don't they? So, they're equal.
[A white dotted line runs vertically down the image, separating either half of the orange. Text appears on either side of the line: 1 half.]
Mathematicians, I think we've got a name for this, because we know that when we partition a whole into two equal parts, we can call them a half. So, we have one half and we have another half of the orange. And now when I'm thinking about what's the same about all these images, I'm seeing something really interesting. Are you?
[A black dotted line runs horizontally across the bead image, separating the pink from the green beads.]
Yeah, because if we look at our beads and we partitioned them to show the pink beads and the green beads, yeah, there's the same number of beads in each part.
[Text appears on either side of the dotted line: 1 half.]
And so, we could call the pink beads one half of our collection of beads and the green beads as one half of our collection of beads. Ah, yes. And it's the same with the muffins, isn't it?
[A white dotted line appears in the muffin image, separating the pink muffins from the blueberry muffins. Text appears on either side of the dotted line: 1 half.]
Yeah, because we have six pink muffins out of our 12, so that's one half, and then we have six blueberry muffins, which is the same number of muffins. So, we can also call that a half. So, maybe all of these images are showing halves. OK. This is our final image. Let's see what we notice and what's the same. Eyeballs ready? OK, here we go.
[In the top left section, four rectangular shapes appear as part of a bigger rectangle. The shapes alternate in colour between blue and orange. The left most rectangle is blue and the right most rectangle is orange.]
Oh. What are you noticing, mathematicians? Pause the video and press play after you've written down your thinking.
[A black outline appears around the large rectangle. Black outlines appear around the smaller, individually coloured rectangles.]
Oh, yeah. I can see that too. It looks like we have one large rectangle, but then inside that rectangle are four smaller rectangles. Yeah, and they all look like they're the same size as each other, don't they? Yeah, so, four equal parts.
[The black outlines disappear, and same-coloured outlines and shading appear for the smaller rectangles]
Yes, and two of those parts are blue and two are orange. But when I'm thinking about what's the same with this image and the others, I'm feeling a little bit confused. Are you? Yeah, because we were thinking that all of these images showed halves, two equal parts of a whole. But now looking at this new image, I can see four equal parts, not just two. So, I wonder if this image is showing halves or not. This feels like my brain's getting a little bit sweaty, and I think we might need to investigate.
[White text on blue background: Let’s investigate! On a table is a piece of yellow card and a sheet of A4 paper. The speaker’s hands are visible. She holds a small, paper copy of the blue and orange rectangle image.]
So, we're wondering whether this image is actually showing halves. Has this rectangle been halved or not?
[The speaker places the blue and orange image on the yellow card and picks up the A4 piece of paper.]
So, to investigate, I thought we could recreate the image using this piece of A4 paper. Now, I can see in the image that there are one, two, three, four equal parts. So, I need to divide my paper into four equal parts.
[The speaker folds the A4 paper lengthways in half. She unfolds the paper and points to either side of the crease to demonstrate the equal halves. She then refolds the paper, and folds that half in half again to create equal quarters.]
So, I know that if I halve my sheet of paper like this, I will have two equal parts. But if I halve my half, I will have four equal parts. Yes. Or quarters. So, now I've got my four equal parts. I need to use colour like the image.
[The speaker unfolds the paper to show the quarters. In fast-forward, she colours in the quarters to match the original image. From left to right they are blue, orange, blue, orange.]
Alright. So, our question, though, mathematicians, is, is this showing halves? Has this piece of paper been halved?
[The speaker covers the coloured quarters with same size and same colour cut-outs of paper.]
So, to help us out, I have cut out four equal sections of pieces of coloured paper that are exactly the same size as our four equal parts of our whole rectangle. Now, to determine whether these are halves or not, we need to think about what we know about halves. And we know that halves are two equal parts of a whole. So, if this is our whole, each of our halves should be the same size. And then I remembered that I could use my mathematical imagination to help me out. I can imagine the blue parts coming together and the orange parts coming together. Can you visualise that, mathematicians? Yes. So, this is what it looked like in my mind.
[The speaker slides off the second-from-left orange paper and swaps it with the blue paper on its right. This means that the left half of the paper is all blue and the right half of the paper is all orange.]
I imagined moving the orange piece to where the blue section was and then moving that blue part to where the orange was. Can you see that, mathematicians? Yes, it's much clearer to see now that we actually look like we do have halves. It looks like half of our paper is orange and half is blue. But just to be sure, we need to make sure that they're the same size.
[The speaker picks up both pieces of blue paper and places them on the orange pieces.]
And so, we can use direct comparison by sliding those two parts across and checking that they are the same size or cover the same area. And they do.
[The speaker returns the coloured paper to their original positions.]
So, that means that our image is, in fact, showing halves.
[On the table is the speaker’s quartered and coloured A4 paper and a stack of blank A4 paper.]
So, this got me thinking, mathematicians, if this is one way that we can halve a piece of paper, I wonder what other ways we can find.
[The speaker places a pair of scissors and some coloured markers on the table. She then folds a piece of paper from the stack.]
You could cut, you could colour, or you could fold. Sounds like a great mathematical investigation to me.
[White text on blue slide: Over to you mathematicians…
- How many different ways can you halve an A4 sheet of paper?
- How will you know if they are halves?]
So, it's over to you, mathematicians. How many different ways can you halve an A4 sheet of paper? And how will you know if they're halves? Have fun.
[The NSW Government logo flashes on screen. Text below reads: Copyright, State of New South Wales (Department of Education), 2021.]
[End of transcript]
Instructions
- Watch the video and write down or draw what you notice about each image.
- Write down or draw what’s the same about the images.


- How many different ways can you half a piece of A4 paper.? You could cut, draw, colour or fold to show your halves.
- How will you know if they are halves?
- How will you know if they are halves?
- Get creative and have fun!
Discuss and reflect
- How could you convince someone that you have halved your piece of paper?
- How could you prove if the piece of paper has been halved or not?
Paper halving – part 2
Watch Paper halving – part 2 video (13:46).
[Bold, white text on a dark blue background: Paper halving – part 2. From NRICH. In the bottom right corner is the red waratah logo of the NSW Government. In the bottom left corner is the text NSW Mathematics Strategy Professional Learning team (NSWMS PL team)
A piece of yellow card is on a table. Five pieces of A4 paper are laid out on the yellow paper, with dark lines indicating folds in the papers. The top right paper is divided in to four equal sections. The top left and bottom right section are coloured in purple while the top right and bottom left are coloured in green. The speaker is off-screen, but her hands are visible. She waves over the table.]
Speaker
Welcome back, mathematicians. How did you go? I've been having lots of fun playing around with finding different ways to halve a piece of paper, and I think I've found some halves. But you are very right. As mathematicians, we need to be able to prove our thinking.
[The speaker collects up all four pieces of paper in to one stack and places them off screen. The remaining piece of paper is presented in portrait with a dark line and fold placed vertically down the middle.]
And so, I started wondering how I could prove that each of my sheets of paper were, in fact, halved. And so, I started with this one, and I thought about what I know about halves, and halves are two equal parts of a whole. And so, if I indeed do have halves here, they should be exactly the same size.
[The speaker folds the piece of paper across the middle, vertical line.]
And so, I used paper folding to help me prove it.
[The speaker lifts up the bottom corner of the folded paper and touches the long edge of the top half. The then touches the long edge of the bottom half before picking up the paper from the fold and showing that the two edges are perfectly aligned.]
And when I fold this edge of the paper to this edge, you can see that it joins up perfectly.
[The speaker touches the bottom corner and the top corner and turns the paper over. She then unfolds it and places it back on the table.]
Each corner to each corner. And there's no overlap or extra bits of paper. And so, I can pretty safely say that I have proved that I have two halves.
[The speaker gets a pairs of scissors and cuts down the fold.]
If I really wanted to make sure that I had proved that, I could also cut. So, I'm going to cut along this line.
[The speaker finishes cutting. There are now two equally sized pieces of paper, halves of the original A4 piece. She places one half above the other on the table.]
So, I have partitioned my whole into two halves. I have one half and I have another half, and I can prove through direct comparison by sliding one on top of each other that they are, in fact, exactly the same size.
[The speaker gets a green A4 piece of paper and places the two halves of white paper on top of it. The speaker slides one half of white paper over the other which reveals an equally sized half of the green paper.]
If I put a sheet of paper underneath, that makes it even clearer. It's exactly the same size as my whole rectangle. And you can see that when I slide this one on top of the other, I have one half of my whole, and they are equal in size. So, yes, I have found one way to halve my piece of paper.
[The speaker discards the white halves and the green paper. The speaker takes of the piece of paper in landscape divided in four with coloured in purple and green sections. The green sections are in the top right and bottom left. The purples sections are the top left and bottom right.]
Then I had a look at this one, and I was pretty proud of this because I have divided my whole into four equal parts and I've coloured two of those parts in green and two in purple. And I want to be able to prove that each part is the same size. So, I'm saying that I have one half that is purple and one half that is green.
[The speaker collects a stack of small, blue paper tiles. She starts to cover the top left purple section with the smaller blue tiles.]
So, one way that I know that I can do that is by comparing their area, and I know that area can be compared by using a unit and repeating that unit so that there's no gaps or overlaps.
[Four small blue tiles completely cover the larger purple section.]
So, here I can see that one purple section can be covered by four tiles. We have one row of two, and two rows of two, four.
[The speaker covers the bottom right purple section with four blue tiles.]
And this purple section can also be covered, yes, with four tiles as well. So, we know that both of the purple sections are equal, which means that they're equal parts. But I wonder if our two purple sections are equivalent to our two green sections.
[The speaker slides the four blue tiles from the bottom right purple section to the top right green section.]
So, I'm gonna slide my tiles up here. Three. Four, look at that. So, my green section is the same size as my purple section. Four tiles covers the surface area.
[The speaker slides the four blue tiles from the top left purple section to the bottom left green section.]
And again here. So, that means that we need a total of four and four, so eight tiles to cover the green of our sheet of paper and a total of eight tiles to cover the purple section.
[The speaker moves the eight blues tiles back to the purple sections before taking the off the paper entirely and placing them in a vertical rectangular shape beneath the paper.]
So, that means that two of my quarters is the same as one half of my whole. And I could show you that using direct comparison as well, couldn't I?
[The speaker discards the blue tiles and cuts the paper in to four sections, two purple and two green and arranges them so that they are in the same spots before they were cut.]
Yeah. So, I could cut. And I could use my mathematical imagination again to bring the purple parts together and the green parts together. Yeah. Can you see that, like this?
[The speaker swaps the bottom right purple square with the bottom left green square. The two purple squares and the two green squares are now on top of each other.]
And so, I can see that half of my piece of paper, of my whole, is green, and half is purple.
[Two A4 pieces of paper in landscape with dark, diagonal lines and equivalent folds are now on the table.]
Now, let's have a look at these two. Now, I'm not sure about these two. I started to get a little bit creative with my halving, and so, I want to be able to figure out if these two parts are the same size so they're halves, and if these two parts are the same size so they're halves. And just by looking at it, I'm finding it really hard to visualise.
[The speaker folds the left-hand side piece of paper along the diagonal fold. It is not an equal match and leaves two triangles of overhanging paper.]
So, I thought I would use my paper folding method from before to fold along the line for that one. But see here, I've got a part that's not covered. Can you see that? And then if I flip it over, yeah, I can see that there's a part that's overhanging. So, that's a bit tricky. Let's have a look at this one.
[The speaker folds the right-hand side piece of paper along the diagonal fold which also leaves and excess of overhanging paper.]
Fold that one over. Yeah, see this, again? Same thing. I've got a part of the paper that hasn't been covered. And then if I flip it over, I've got this section that's hanging over. What do you notice about these two pieces of paper in the way I've folded them? Yeah, I'm seeing that too. Can you see, this section here, that shape that that's making, it's a triangle, isn't it?
[The speaker flips the right-hand side folded piece of paper over and outlines two identical uncovered triangles on other side.]
With three sides. Looks like, if I rotate it this way, it actually looks like it could be the same size as that triangle, can you see that? So, that's making me think that maybe I can use that.
[The speaker flips the right-hand side folded piece of paper over to show two unequal uncovered sections.]
But this section that's not covered doesn't look the same at all to this section hanging over, does it? It looks very different. So, I wonder if that's going to give me a clue.
[The speaker unfolds both pieces of paper.]
Mathematicians, how else could I prove or disprove that these are halves? Yes, I could use cutting, couldn't I? And then direct comparison. So, let's have a look. So, if I cut along here.
[The speaker uses scissors to cut along the fold of the left-hand side piece of paper.]
So, I've partitioned that into two parts. I cut along here, and partition that piece into two parts.
[The speaker cuts along the fold of the right-hand side piece of paper.]
Now, to make sure that they're halves, they need to be the same size, don't they? So, I can use direct comparison to try.
[The speaker flips one half of the left-hand side piece of paper top to bottom. She flips the same piece side to side. The flipped piece now matches the un-flipped piece.]
So, I'm going to flip this piece, and then I'm going to flip it again. See that? Yes. And then I'm going to slide it onto the top. And look at that, it fits.
[The speaker places one half above the other on the table.]
So, this proves that these are two halves of our whole. Let's do the same with this one.
[With the right-hand side halves, the speaker flips on half top to bottom and then side to side. She places the flipped half on the un-flipped half. They are unequal in size.]
So, I'm going to flip, and I'm going to flip again and then I'm gonna slide. What do you notice? Yeah, I see that too. It's not covering the whole area, is it? So, these two pieces are not the same size. Yeah.
[The speaker places one half above the other, before returning the two halves back to their original position.]
OK. So, that means that this piece of paper that I thought I might have halved like this is actually not halved, because our parts aren't equal.
[The speaker returns the left-hand side piece of paper back to its original position.]
OK. But this piece of paper, which I had halved like this, is halved because there are two parts and they're equal. I'm gonna put this one away.
[On the table is an A4 piece of paper in landscape with folds to make even eighths. A dark line which starts a quarter of the way up the left edge of the paper, runs horizontally along to the middle and then vertically three-quarters up and the to the right to the other edge of the paper.]
I was very proud of this one, because, yeah, it makes a really different shape to the others, doesn't it? And so, to figure out whether this is halved, I'm going to use my cutting and direct comparison technique again.
[The speaker slides a landscape piece of green paper underneath the folded white piece.]
And to make it really clear, I'm going to put this piece of paper that's exactly the same area as my white piece of paper underneath. So, going to cut this shape out.
[The speaker cuts along the dark line and the puts the two halves back together over the green paper.]
OK. So, here are what I think are my two halves.
[The speaker flips one half top to bottom and then side to side and places the flipped half over the un-flipped half. The two halves match perfectly.]
And then to make sure, I'm going to flip and I'm going to flip and I'm gonna slide. Look at that. Yes. You can see that these are two halves because they're exactly the same size and you can see the shape of the whole underneath.
[The speaker traces around the green half, before returning both halves to their original position.]
And so, I have two halves that made a whole.
[All four pieces of paper which were successful halved are on the table.]
So, there we have it, mathematicians. We've come up with some really creative ways to halve a piece of paper and then to prove or disprove whether or not we have two equal parts of a whole. And so, I was really excited, and I was talking to one of my mathematician friends about this, and they came up with a really interesting idea of how they could halve a piece of paper, and it looks like this.
[The speaker clears away the existing pieces of paper and places on the table an A4 piece of paper in landscape. This piece has been folded to create triangle where the bottom edge of the triangle is the entire bottom edge of the paper, and the top point is halfway between the top edge. The triangle is coloured in blue and the remaining area of the paper is coloured in red.]
What do you notice? Yeah. And they said to me, I'm really excited, but I just can't figure out how to prove whether or not I've halved my piece of paper. And so, I thought that you could help us out, mathematicians.
[Bold white text on a blue background: Over to you mathematicians… In small font in the top left corner is the text: NSW Department of Education.]
So, it's over to you. How could we prove whether or not this piece of paper has been halved?
[The blue and red triangle piece of paper is on the table.]
Have fun investigating.
[Bold white text on a blue background: What’s (some of) the mathematics?]
So, what's some of the mathematics?
[Dark text on a white background: What’s (some of) the mathematics? We notice that halves are two equal parts of a whole.]
We notice that halves are two equal parts of a whole.
[Dark text on a white background: Halves can look different but, as long as they are two equal parts of a whole, they still have the same value. For example,]
Halves can look really different, but as long as they are two equal parts of a whole, they still have the same value. For example…
[Dark text on a white background: We can halve a whole object. Beside the text is an image of an orange cut in half with a vertical dotted line running down the middle. Above each orange half is the text: 1 half.
[An image of a the vertically halved piece of paper]
We can halve a whole object like our orange or like our piece of paper.
[Dark text on a white background We can also halve a collection of objects. An image of five red balls and five green balls connected by a piece of string. A dotted line runs horizontally across the image, dividing the red balls and the green balls. On both sides of the dotted line is the text: 1 half.
An image of a tray of muffins. Six muffins have pink icing and six are un-iced. A white dotted line runs vertically down the middle dividing the iced from the uniced muffins. On both sides of the dotted line is the text: 1 half.]
We can also have a collection of objects, like our beads and our muffins. As long as there are the same number of objects in each part, then they're halves.
[New slide. Dark text on white background: What’s (some of) the mathematics? We can also halve the same object in lots of different ways. Even though these halves may look really different, we know the object has been halved because it is now partitioned into two equal parts.
Five pictures appear of the papers halved in different ways.]
We can also halve the same object in lots of different ways. And even though these halves may look really different, we know the object has been halved because it's now partitioned into two equal parts.
[New slide. Dark text on white background: What’s (some of) the mathematics? As mathematicians, we investigate problems and proved our thinking in lots of different ways.
An image of four vertical paper rectangles alternate blue and orange colour. The rectangles together are the same size as a landscape A4 piece of paper.]
We've also learnt that as mathematicians we investigate problems and prove our thinking in lots of different ways.
[The middle two blue and orange rectangles swap so that they form two same-coloured halves.]
Today we used our mathematical imaginations to visualise the two colours coming together and prove that we had two halves because they were the same size.
[An image of a hands holding a A4 piece of paper vertically down the middle.]
We also used a paper folding technique so we could use direct comparison to prove that our two parts were the same size.
[An image of the paper folded in eighths cut in halves and placed on top of each other to show the equally sized green paper underneath.]
We used a cutting technique so we could place one half on top of the other and prove that it was the same size.
[An image of the purple and green coloured piece of paper divided in to four sections with the smaller sized blue tiles covering two opposite sections so that only the green-coloured sections remain. The tiles swap position so that the purple section is exposed.]
And we used indirect comparison by using paper tiling to prove that the purple parts were the same size as the green.
[The NSW Government logo flashes on screen. Text below reads: Copyright, State of New South Wales (Department of Education), 2021.]
[End of transcript]
Instructions
- Watch the video to see some ways to prove if a piece of paper has been halved or not.
- Can you find a way to prove if the piece of paper in the image has been halved or not?


Paper halving – part 3
Watch Paper halving – part 3 video (5:05).
[A title over a navy-blue background: Paper halving - part 3. Below the title is text: From NRICH. Small font text in the lower left-hand corner reads: NSW Mathematics Strategy Professional Learning team (NSWMS PL team). In the lower right-hand corner is the red waratah of the NSW Government logo.
The speaker waves her hand.]
Speaker
Welcome back, how did you go?
[On a table is a large yellow sheet. On the sheet is a piece of paper that has been divided into 3 triangles. On the left and right sides of the paper are 2 triangles with red squiggles inside. In between these is a triangle with blue squiggles inside.]
When I left you, we were trying to figure out a way of proving whether or not this piece of paper had been halved. And when I was looking at this, I started thinking, well, I might try to use the folding technique to help me out. And so…
[She folds the paper from the top right corner down – folding the right ‘red’ triangle in.]
…I folded along these lines like this and then like this.
[She folds the paper from the top left corner down – folding the left ‘red’ triangle in.]
But I noticed that I had a bit of a problem. Do you see what it is, mathematicians?
[She unfolds the left flap.]
Yeah, there's this overlap because this shape is overlapping with this…
[She unfolds the right flap.]
…triangle, and so it's hard to compare whether they're actually the same size. And plus, there's this…
[She points to the ‘blue’ triangle.]
…other triangle shape down here, which hasn't even been covered. And so…
[She unfolds the paper.]
…that's not going to help us out. So I started to think about how I might be able to show this using direct comparison.
[She brings out an orange triangular paper and places it over the right triangle.]
And so I've cut out some more pieces of coloured paper that are exactly the same size as our three parts…
[She places another orange triangular paper over the left triangle.]
…like this.
[She places a blue triangular paper over the middle triangle.]
And, I remembered again that I could use my mathematical imagination to visualise these shapes moving. Can you see that?
Yeah. What would you move mathematicians to help us figure out whether we have halves. Oh, yes, I thought that too. So I decided to move these…
[She holds up the orange triangles.]
…two triangles in my mind to see whether they were the same size as the blue triangle.
[She puts down the orange triangles.]
Because then we would have halves, half orange and half blue. And so I flipped…
[She flips the triangle on the right top to bottom.]
…this triangle and then flipped it again…
[She flips the triangle right to left.]
…and I slid it into place here.
[She aligns the triangle over the right side of the blue triangle.]
Yes, can you see that? Already, I'm seeing that it looks like the orange triangle covers half of the surface area of the blue. So let's try this one. We're going to flip…
[She flips the triangle on the left top to bottom.]
…and then we're going to flip again…
[She flips the triangle left to right.]
…and slide.
[She aligns the triangle over the left side of the blue triangle.]
Ah-ha! Look at that, mathematicians! Yes, they're the same size. So that must mean that we have actually halved...
[She places the orange triangle back into the ‘red’ areas.]
…our piece of paper. Half is orange and half is blue. I wonder what would happen if I flipped…
[She flips the triangles top to bottom.]
…and flipped again…
[She flips the triangle outside in.]
…and then joined these two triangles.
[She pushes the orange triangles together. Then she moves the blue triangle down and joins it with the two orange triangles.]
Oh, look at that, yeah, it's a parallelogram.
[She traces the edges of the shape.]
And I can see really clearly that half is orange and half is blue.
[Title over a blue background: Over to you mathematicians…
Below the title is a numbered list:
- How many ways we can find to fourth (quarter) a piece of paper?
- How many ways can you eighth a piece of paper?
- How will you know if we have quarters and eighths?]
So this got me thinking mathematicians, we've found lots of different ways to halve a piece of paper.
So I wonder how many ways we can find to fourth or quarter a piece of paper? And then how many ways can we eighth a piece of paper? And finally, how do we know if we have quarters and eighths? So it's over to you mathematicians, have fun investigating.
[Text over a blue background: What’s (some of) the mathematics?]
Just before you go, mathematicians, let's have a look at what some of the mathematics is that we have been learning.
[A title on a white background reads: What’s (some of) the mathematics?
Text below reads: We can also halve the same object in lots of different ways. Even though these halves may look really different, we know the object has been halved because it is now partitioned into two equal parts.
Below the text are 2 rows of images. The top row has an image of a white paper with a line down the middle; a paper that has a line down the middle and across creating 4 smaller rectangles that have been coloured in; and a white paper that has a diagonal line about a quarter towards each end of the paper. The bottom row has an image of 4 strips of alternating blue and orange papers next to each other and an image of a white paper with a geometric line that goes across it.]
Do you remember yesterday when we learnt that one object can be halved in lots of different ways? And that we know that even though these halves look really different, we know that the object is being halved because it's now partitioned into two equal parts.
[A title on a white background reads: What’s (some of) the mathematics?
Text below reads: Even though halves may look different, we know the object has been halved because it is now partitioned into two equal parts.
In the bottom left corner is an image of the paper divided into the 3 triangles.]
And so, we used this to help us today to try to prove that this piece of paper that looked really different had been, in fact, halved.
[Next to the image, an image of the paper folded appears.]
So, we noticed that we couldn't use our paper folding technique to prove whether this piece of paper had been halved or not because the edges didn't line off and they overlapped.
[Next to the image, an image of the paper with the coloured papers overlayed it appears.]
And so, we used our mathematical imaginations to flick and…
[The image changed to an image with the right orange triangle over the right side of the blue triangle and the left orange triangle has been pushed up slightly.]
…slide the orange triangles on top of the blue triangle.
[The image changed to an image of the left orange triangle being over the left side of the blue triangle, so that the orange triangles completely cover the blue triangle.]
And we proved that the orange parts are the same size as the blue parts, proved we have halves.
[Over a grey background, the red waratah of the NSW Government logo appears amongst red, white and blue circles. Text: Copyright State of New South Wales (Department of Education), 2021.]
[End of transcript]
Instructions
The video showed one way we could prove if the piece of paper has been halved or not.
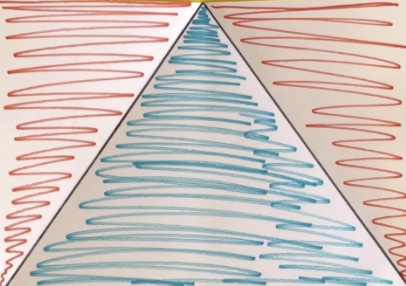

Now that we’ve investigated halving a piece of paper:
- How many ways can you fourth (quarter) a piece of paper?
- How many ways can you eighth a piece of paper?
- Can you find a way to prove if the piece of paper in the image has been halved or not?
- How will you know if you have quarters or eighths?
Discuss and reflect
- How many ways did you fourth (quarter) your piece of paper?
- How many ways did you eighth your piece of paper?
- How can you prove your paper has quarters or eighths?