Introducing rekenreks
A thinking mathematically targeted teaching opportunity focused on exploring the features of a rekenrek and how to use a rekenrek to represent and rename numbers.
Syllabus
Syllabus outcomes and content descriptors from Mathematics K–10 Syllabus (2022) © NSW Education Standards Authority (NESA) for and on behalf of the Crown in right of the State of New South Wales, 2024.
Outcomes
- MAO-WM-01
- MAE-RWN-01
- MAE-RWN-02
- MAE-CSQ-01
- MAE-CSQ-02
- MAO-WM-01
- MA1-RWN-01
- MA1-RWN-02
- MA1-CSQ-01
Collect resources
You will need:
- pencils
- your rekenrek
- your mathematics workbook.
Introducing rekenreks
Watch the Introducing rekenreks video (11:53).
Speaker
Hello there mathematicians. I hope you're having a gorgeous day today.
Let's explore the rekenrek.
So, this is what my rekenrek looks like at home, and here's another one I drew on the computer; and we're going to use the one I drew on the computer to do some mathematical investigating today.
[Screen shows 2 rekenreks. The top rekenrek has 2 rows of beads. On each row there are 5 red beads and 5 blue beads. The bottom rekenrek also has 2 rows of beads. On each row there are 5 red beads and 5 light orange beads.]
Speaker
So, before we get started like great mathematicians, we often ask this question, what do you notice?
[Screen show rekenrek with 2 rows. Both rows contain 5 red beads and 5 light orange beads.]
Speaker
So, before we begin imagining and playing with and thinking about the rekenrek what do you notice about it? What are some of its features?
Ok, so see if you've got one idea. Can you come up with another idea? What else did you notice?
Ah yes, and sometimes we can notice things that aren't mathematical. See if you can notice some mathematical things.
Ok, shall we share some of those ideas together 'cause I can hear some of you saying that you notice that there are different coloured beads?
Yeah, did you notice that too? There's some red beads and there's some light orange beads.
Yes, and that each colour represents a collection of 5.
Look, there's a chunk of red, and there's 5 red beads inside that blue circle. And each chunk of colour represents another 5.
[Screen shows a transparent blue circle. It covers the 5 red beads to show that they are a group of five. Another blue circle covers the 5 light orange beads to show that they are a group of five. The blue circle does the same to the bottom row of the rekenrek.]
Speaker
Yes, there's 5 in there, and that chunk is also 5. Yeah, ah and that led some of you to notice this, that there are 2 fives on the top row.
Look one five, 2 fives and 2 fives on the bottom row. One five, 2 fives.
[Screen shows a blue transparent circle. It groups the 5 red beads on the top row of the rekenrek, followed by the 5 light orange beads. It then moves to the bottom row of the rekenrek and groups together the first 5 red beads and then the last group of 5 light orange beads.]
Speaker
Yes, and some of you said hey, that's the same as saying there are 10 on the top row and 10 on the bottom row. And yes, and that helped us to realise that there are 20 beads in total.
[Screen shows the transparent blue circle grouping the 10 beads on the top row together, then the 10 beads on the bottom row together.]
Speaker
All right, then I was thinking if we're introducing rekenreks, well, how can we use rekenreks? How can we use them?
So, let's have a look.
Yes, and what we do is we move beads across to represent quantities.
So, at the moment over here there's there are no beads, so my rekenrek is representing zero.
[Screen shows rekenrek with 2 rows. The top row has 5 red beads and 5 yellow beads. The bottom row is the same as the top row. A blue transparent circle appears on the left to signify the starting point of the rekenrek.]
Speaker
But if I move one across over here now, I'm representing the quantity of one.
[Screen shows one red bead from the top row moving across to the left side of the rekenrek.]
Speaker
Yes, what about if I do this and move another bead across?
[Screen shows the presenter moving another red bead across from the top row of the rekenrek.]
Speaker
Over here I'm now representing 2, Yes. And yes, I can represent 2 in a different way.
[Screen shows the presenter sliding the second bead back to it’s initial position. She moves a bead from the bottom row of the rekenrek to the left side.]
Speaker
In this case, now I'm representing 2 but I have one at the top and one down the bottom.
Ok, mathematicians, I think you're ready.
It's time to start imagining.
Here's my rekenrek, and I'd like to move some beads across, and I'd like you to imagine that I'm moving 5 beads across.
[Screen shows a rekenrek with 2 rows. The top row has 5 red beads and 5 yellow beads. The bottom row is identical to the top row. On the left side of the rekenrek there is a blue transparent circle showing the empty space where the beads will move.]
Speaker
So, close your eyes and use your mathematical imagination to imagine you're moving those 5 beads across my rekenrek, and how are you moving them.
Ok, let's have a look. This is how I imagined it.
[Screen shows the rekenrek. The top row has the 5 red beads pushed over to the left side of the rekenrek, whilst the yellow beads stay in their initial location. The bottom row of the rekenrek stays the same.]
Speaker
Yes, and some of you imagined it like that, but some of you imagined it in a different way.
Yeah, which is also awesome because we can think about things differently. But over here I have 5. Ok, let's get our mathematical imaginations again. Are you ready? And this time I'd like to imagine 4.
[Screen shows the presenter sliding the beads back into place. The top and bottom rows of the rekenrek are now the same, with 5 red beads and 5 yellow beads. On the left side of the rekenrek. There is a blue transparent circle showing the empty space where the beads will move.]
Speaker
So, close your eyes. And in your minds eye, imagine you're touching the rekenrek and yes, I can see it. Put your arms up. Yes, and move across 4 beads.
Ok and let's see if you imagined it in the same way I did. Here's how I imagined it.
[Screen shows 4 red beads on the top row of the rekenrek sliding across to the left.]
Speaker
Ah yes, and I have 4. Ah ha, and some of you like me, thought about this one left behind strategy because we know that chunk of red is a 5 and because 4 is one less than 5, if I just leave one behind, I can slide across 4.
[Screen shows the rekenrek with the 4 red beads of the top row on the left. The leftover red bead is circled with a transparent blue circle.]
Speaker
Yes, the one left behind strategy. Ok, and that helps me to see that 4 is made up of 4 and zero.
Alright.
[Screen shows the 4 red beads on the top row of the rekenrek sliding back over to their initial position.]
Speaker
Let's imagine again, so over here on this time. Let's imagine 4 but in a different way.
Ok, close your eyes.
Imagine the rekenrek and you're sliding across 4 beads. How are you doing it?
Oh. Ok, let's have a look if we imagined it in the same way this time. Here we go.
[Screen shows 2 red beads on the top and bottom row of the rekenrek sliding across to the left.]
Speaker
Oh yes, I had 4 as double 2 and some of you thought about it like that way too
Yes, and I took away their highlighting 'cause I think we know what area to attend to now we're Ok.
Alright, let's slide those beads back.
[Screen shows beads sliding back to the right.]
Speaker
Ok, and why not? Let's keep playing with 4.
So, close your eyes mathematicians and imagine 4 moving across but in a different way again.
Oh, ok, and some of you are moving some beads on the top and some of you are moving some beads down the bottom.
I can see you're imagining it. Ok, let's have a look together. Did we imagine it in the same way? Ready? Ah ha, some of you did. We had 4 as 3 and one.
[Screen shows 3 red beads on the top row sliding to the left and one red bead on the bottom row sliding to the left. Afterwards, the beads slide back over to their initial position.]
Speaker
Ok, let's try again ready? Um, yeah, let's think about 4 in another new way. So, imagine it in your mind's eye.
You're moving beads across. Ah ha. Ok, let's have a look together. Is that what you imagined?
[Screen shows one red bead on the top row sliding to the left and 3 red beads on the bottom row sliding to the left.]
Speaker
Oh, some yes and some still no. That's Ok, mathematicians. It's still 4. Yes, and in this case, we have one and 3.
Yeah, and actually this is making me realise something which is, I think, pretty cool. Rekenreks can help us see important things about numbers
So, for example, we can see the smaller numbers that hide inside the bigger numbers. Look.
Here's where we have, we were thinking about 4 and we can see 4 is 4 and zero. We can see 4 is 3 and one. We can see 4 is double 2, 2 and 2. And we could also see 4 as one and 3.
[Screen shows 4 separate rekenreks. On the top right of the page it says ‘4 is…’. All of the rekenreks have two rows with 5 red beads and 5 yellow beads.
The top row of the first rekenrek has 4 red beads pushed over to the left, whilst the rest of the rekenrek stays the same. On the right it says 4 is 4 and 0.
The second rekenrek has 3 red beads on the top row to the left and one red bead on the bottom row to the left. On the right it says 4 is 3 and 1.
The third rekenrek has 2 red beads to the left on both the top and bottom rows. On the right it says 4 is 2 and 2.
The final rekenrek has 1 red bead on the top row to the left, and 3 red beads on the bottom row on the left. It says 4 is 1 and 3.]
Speaker
And yeah, can you see that pattern too? Look? Look at the, look over at the left over here.
There's 4 at the top and zero at the bottom.
[Screen shows blue circle highlighting the left side of the first rekenrek, showing the 4 red beads to the left of the first row.]
Speaker
Then there's 3 at the top and one at the bottom.
[Screen shows blue circle highlighting the left side of the second rekenrek, showing the 3 red beads to the left of the top row and the single red bead to the left of the bottom row.]
Speaker
And yes, 2 at the top and 2 at the bottom and one at the top and 3 at the bottom.
[Screen shows blue circle highlighting the left side of the third rekenrek, showing the 2 red beads to the left of the top row and 2 red beads to the left of the bottom row. Finally, the blue circle highlights the left side of the fourth rekenrek, showing the single red bead to the left of the top row and the 3 red beads to the left of the bottom row.]
Speaker
Yes, and if you just look at the top numbers. Look. 4, 3, 2, one. Yes, like the pattern in the backward count.
[Screen shows blue circle highlighting the first rekenrek down to the fourth rekenrek to show the decreasing number of red beads on the top rows.]
Speaker
Ok mathematicians, I think there's another way that we could make 4 still. So, let's imagine it.
Let's close our eyes and imagine what 4 could look like on a rekenrek that we haven't done yet. Are you imagining it?
That idea of the pattern and the backward count on the top row might have helped you.
Ok, pick up your pencil mathematicians. And draw it on a piece of paper.
What do you think another way of representing 4 on the rekenrek might have looked like? There's a new way we haven't done yet.
You're thinking hard I can see. That's right, 'cause we had one where we had 4 at the top and zero at the bottom.
Then 3 at the top and one at the bottom. 2 at the top and 2 at the bottom. One at the top and 3 at the bottom.
Yes, and this time the pattern if we kept going with it, there would be zero at the top and 4 at the bottom. Yes, it would look a little bit like this.
[Screen shows rekenrek the top row stays the same, but the bottom row has 4 red beads pushed to the left.]
Speaker
Uh-huh is that what you imagined and drew?
Yes, and you're right. We could use that one left behind strategy again, 'cause we know there's a chunk of 5 and 4 is one less than 5.
So, we can just leave one behind and slide the others over. And voila, we know that's 4. I know it's a little bit like mathematical magic.
Ok, so mathematicians here's your challenge.
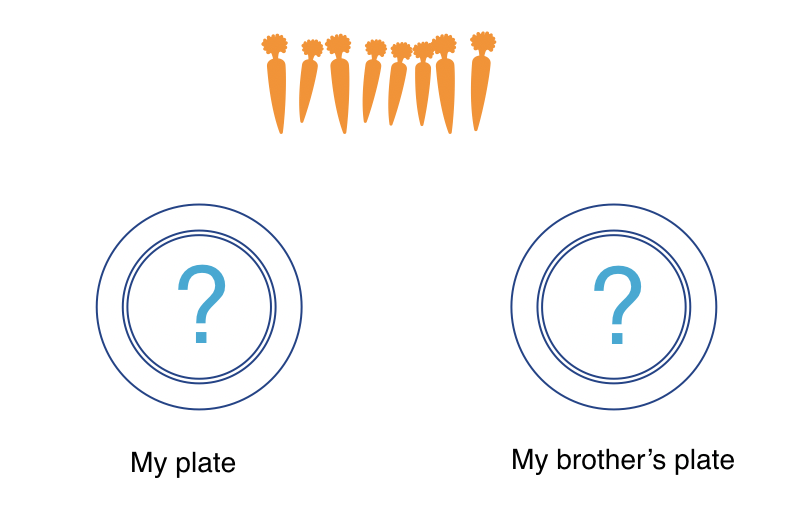
I'd like you to think about this problem with me. So, mum gave us some baby carrots for a snack. There were 8 in total. Some carrots were on my brother’s plate and some carrots were on my plate.
So here are the baby carrots or a picture of the baby carrots. And here's a picture of my brother's plate. And here's a picture of my plate.
[Screen shows a picture of 8 carrots. Underneath the carrots there are 2 plates. The left plate has a question mark inside of it with My plate written underneath it. The right plate has a question mark inside of it with My Brother’s plate written underneath it.]
Speaker
And we can also use the rekenrek to help us imagine solving this problem too.
[Screen now shows a rekenrek underneath the plates. The top and the bottom rows of the rekenrek have 5 red beads and 5 yellow beads.]
Speaker
Yeah, 'cause we know we have 8 carrots and if I slide 8 carrots across, I could say those 8 carrots represent what's on my plate and the ones down the bottom represent what's on my brother’s plate, which is zero.
[Screen reads: Mum gave us some baby carrots for a snack. There were 8 in total. Some carrots were on my brother’s plate and some carrots were on my plate.
Screen shows a rekenrek underneath with 5 red beads and 5 yellow beads on the top and bottom rows. As the speaker talks, 8 beads on the top row made up of 5 red beads and 3 yellow beads slide across to the left side.]
Speaker
And then I can draw a picture to record my thinking like a mathematician.
[Screen shows a hand drawn rekenrek. The top row shows 8 beads made up of 5 red beads and 3 yellow beads on the left side. The rest of the rekenrek remains the same. On the top right ‘8 is…’ is written and to the right of the rekenrek ‘8 is 8 and zero’ is written.]
Speaker
So, mathematicians, it's now over to you. How many carrots were on my plate? How many carrots were on my brother's plate? And show as many solutions as you can.
OK mathematicians over to you.
So, what's some of the mathematics here?
[Screen shows 5 separate rekenreks. On the top right of the page it says ‘4 is…’. All of the rekenreks have two rows with 5 red beads and 5 yellow beads.
The top row of the first rekenrek has 4 red beads pushed over to the left, whilst the rest of the rekenrek stays the same. On the right it says 4 is 4 and 0.
The second rekenrek has 3 red beads on the top row to the left and one red bead on the bottom row to the left. On the right it says 4 is 3 and 1.
The third rekenrek has 2 red beads to the left on both the top and bottom rows. On the right it says 4 is 2 and 2.
The fourth rekenrek has 1 red bead on the top row to the left, and 3 red beads on the bottom row on the left. It says 4 is 1 and 3.
The final rekenrek has no beads on the top row to the left, and 4 red beads on the bottom row to the left. It says 4 is 4 and zero.]
Speaker
So, what the rekenreks can help us see is that bigger numbers are made up of smaller numbers, so we can see that inside a 4 there's 4 and zero.
But we can also see sitting inside of 4 is 3 and one. 4 is also 2 and 2. Inside of 4 is one and 3.
And we also started to play around with this idea today that when each chunk of colour represents 5.
We can make 4 by thinking about one left behind. And that's a really interesting strategy for us to explore.
OK, mathematicians, have a lovely day. See you next time.
[End of transcript]
Instructions
After watching the video think about this problem, mum gave us some baby carrots for a snack. There were 8 in total. Some carrots were on my brother's plate and some carrots were on my plate.
- How many carrots might have been on my plate?
- How many carrots might have been on my brother’s plate?
- Find as many solutions as you can.
- You can use your rekenrek to help you solve the problem.
- Then, record your thinking.
- You can use your rekenrek to help you solve the problem.