Math mobiles – Stage 3
A thinking mathematically targeted teaching opportunity focussed on investigating unknown values using equivalence
Adapted from a task by Boaler, J., Munson, J., & Williams, C. (2019). Mindset Mathematics: Visualizing and Investigating Big Ideas, Grade 6 (1st ed.). Jossey-Bass.
Images reproduced with permission of John Wiley & Sons, Inc.
Syllabus
Syllabus outcomes and content descriptors from Mathematics K–10 Syllabus © NSW Education Standards Authority (NESA) for and on behalf of the Crown in right of the State of New South Wales, 2023
Outcomes
- MAO-WM-01
- MA3-AR-01
- MA3-MR-01
- MA3-MR-02
- MA3-RQF-02
Watch
Watch Math mobiles video part 1 (10:35).
[Bold, white text on a dark blue background: Maths mobiles. Boaler, Munson & Williams, 2019. In the bottom right corner is the red waratah logo of the NSW Government. In the bottom left corner in small font text: NSW Mathematics Strategy Professional Learning team (NSWMS PL team)]
Speaker
Hi there mathematicians. Today we're going to be investigating Maths mobiles, and these come from Boaler, Munson and Williams.
[New slide. Text: You will need…
Something to write on
Something to write with.
To the right of the text is an image of two sheets of white A4 paper on a table with three coloured markers.]
Speaker
For today you'll need, something to write on and something to write with.
[New slide. Text: What do you notice?]
Speaker
Alright mathematicians, I've got a really great puzzle for us to puzzle over today. I'm going to show you an image, and your job is to write down everything you notice. Are you ready? Here we go.
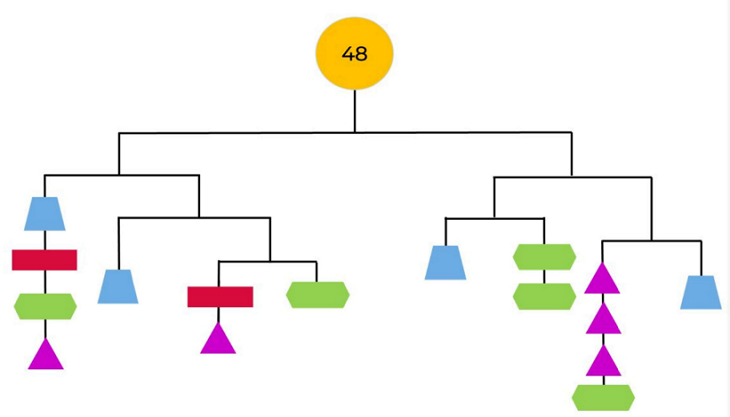
[New slide. An image of a family tree like structure.
At the top is the number 48 in a yellow circle. Horizontal lines branch off into two sections.
The left-hand branch consists of three sub-branches. The left-most branch has two further branches, to the left a string of four shapes. From the top they are a blue trapezium, a red rectangle, a green hexagon and a pink triangle. To the right is another sub-section which on the left has a blue trapezium and on the right is a final sub-branch. To the left of this final sub-branch is a red rectangle and a pink triangle and on the right is a green hexagon.
The right hand branch descending from the 48 are two sub-branches. The left sub-branch has two strings of shapes. The left string is a blue trapezium and the right string is 2 green hexagons. The right-hand sub-branch has a left string of 3 pink triangles and a green hexagon and the right string is a blue trapezium.]
Speaker
It's really interesting, isn't it? Alright, pause the video now and write down everything you notice. And when you're ready, press play and we'll investigate.
[New slide. Text: Let’s investigate.
On a piece of butchers paper, a printed copy of the image is placed in the top left hand corner.]
Speaker
Welcome back mathematicians. How did you go with your noticing? Yeah, I bet you've noticed some really interesting relationships in this diagram, I know I have. Shall we record our thinking?
[The speaker writes Notice? In the top right corner.]
Speaker
Yeah, 'cause we know that mathematicians like to record their thinking 'cause it makes it easier to see patterns and relationships. So what was the first thing you noticed? Ah, yes, some of you are saying that you noticed the shapes first and noticed that there were lots of different types of shapes and so did I. And I thought that we could sort the shapes into their types.
[The speaker points to the 5 pink triangles. Below the text: Notice? She writes the number 5 and then draws a triangle in pink marker. Below that she writes the number 2 and draws a rectangle in red marker.]
Speaker
So, we have this triangle and we've got two and three more, so we have five of these pink triangles, and yes, we've got just two of these red rectangles.
[Below the rectangles, she writes the number 4 and then draws a trapezium in blue marker.]
Speaker
And what have you got here, this blue one, there's one, two, three, four. Yes, they're trapeziums aren't they? Because they're quadrilaterals with two parallel sides. So we have four trapeziums and...
[Below the trapezium she writes the number 4 and draws a hexagon in green marker.]
Speaker
Oh, the green, one, two, three, four, five, five of these green, what could we call this shape? Yes, you're right, it's a hexagon, isn't it? 'Cause it has six sides and that means six angles, so we call it a hexagon, fantastic. So we've got all of these different shapes... Ah, yes, now, some of you also noticed that each of the triangles are exactly the same as the other triangles, so they're the same as each other.
[Beside where she has written 5 and drawn the pink triangles, the speaker writes the text: equivalent.]
Speaker
And we could record that as equivalent 'cause that just means the same as. So the triangles are all equivalent to each other. And it's the same for all the shapes, isn't it?
[She writes the word equivalent beside each shape in the same coloured marker.]
Speaker
The rectangles are all equivalent and the trapeziums are equivalent and so are the hexagons. So we've figured out that there's lots of different shapes and that we can record them like this. What else did you notice? Yes, I was also really interested in all of these lines, because the lines seem to be connecting all of the shapes in different ways, don't they?
[The speaker writes: Lines connecting different shapes.]
Speaker
So we can see that there are lines and they're connecting the different shapes. And did you notice anything else about those lines? Yeah, I was also really interested in that because they're straight, aren't they? And when I look at this entire image, it reminds me of a mobile, that's hanging.
[The speaker picks up the paper and holds it upright, as if the 48 would be holding up all the shapes.]
Speaker
So if we were to hang it up like that, it looks like all of these lines are balanced because they are directly horizontal like this. So it's sort of saying that there are different balance relationships here.
[The speaker adds to the line of text so that the sentence reads: Lines connecting different shapes showing balance (equivalence).]
Speaker
So we could document that and say the lines connect in different shapes, showing balance. And sometimes we talk about balance as being equivalence. So we could actually say that it's showing equivalence, 'cause if we look at these two sides here in this line, it's saying that these shapes have the same weight as these shapes, and that's why they're balanced, they have the same value or weight. Fantastic. Alright, so then if that's the case, then that must mean that all of these shapes are equivalent in value to all of these shapes, and that's really important, we should document that.
[The speaker writes and equation using digits and hand drawn shapes. 2 trapeziums + 2 rectangles + 2 hexagons + 2 triangles = 2 trapeziums + 3 hexagons + 3 triangles.]
Speaker
So we can say that two of these trapeziums and two of the rectangles and two hexagons and two triangles are equivalent in values to two trapeziums and three hexagons and three triangles. Look at that, balance. Some of you are saying that there are other balance or equivalent relationships here as well, aren't there?
[She draws = below the 48.]
Speaker
So, we're seeing that this part is equivalent in value to that part, but there are other connecting horizontal lines, aren't there? OK, let's try documenting some of those. So here I can see a horizontal line and it's showing that these shapes are balanced with these.
[She points to the right-hand branch and writes an equation. Trapezium + 2 hexagons = 3 triangles + hexagon + trapezium. On the image, she also draws a = between the two halves of the right-hand branch.]
Speaker
So we could say that a trapezium and two hexagons are equivalent in value to this side. So equivalent in value to three triangles and one hexagon and one trapezium. Well, look at that, that's a great equation, isn't it? Are there more relationships like that? There is too. Alright, let's look at this one over here.
[She works on the left-hand side. She draws an = between the halves and writes an equation. Trapezium + rectangle + hexagon + triangle = trapezium + rectangle + triangle + hexagon.]
Speaker
So here I can see another horizontal line, and it's showing that these shapes are balanced with these ones, so let's document that. We've got one trapezium, one rectangle, one hexagon and a triangle are equivalent in value to a trapezium and a rectangle and triangle and a hexagon.. And there's more, aren't there? Yeah, 'cause look, if we look here, I can see that the trapezium is equivalent to all of these shapes as well, so let's document that.
[She points to the right half of the left branch and writes an equation. Trapezium = rectangle + triangle + hexagon.]
Speaker
One trapezium is the same in value as a rectangle and a triangle and a hexagon. That's interesting, isn't it? 'Cause one shape has the same value as all of these shapes. So that's telling me something interesting about this trapezium, that it actually must have a greater value than each of these by themselves.
[She draws an = between the trapezium branch and the rectangle, triangle and hexagon branch. She then draws another = between the rectangle triangle branch and the hexagon. She writes an equation. Rectangle + triangle = hexagon.]
Speaker
That's interesting, that could be useful. Alright, there's more look, here we've got another one. So we've got a rectangle and a triangle is equivalent in value to a hexagon.
[ON the right hand branch, she draws an = between a trapezium and 2 hexagons, writing trapezium = 2 hexagons.]
Speaker
And there's more over here. A trapezium is, a trapezium by itself again. So that conjecture is looking like it might be correct because the trapezium is equivalent in value to two of these hexagons, two of them.
[She draws an = sign between the far right branch. Equation: 3 triangles + hexagon = trapezium.]
Speaker
And here again, the trapezium is by itself. So here we've got three triangles and one hexagon and all together they are equivalent to just one of those trapeziums. Have we got them all? Yeah. Oh, wow, look at all these relationships. There's one thing that we haven't talked about, though, isn't there? Yeah. And I think some of you have been looking at this for quite some time. It's this big circle up here with the 48 on it. Yeah, what do you think that might mean? Yeah, because all of these lines are connected, it sort of shows that the 48 must be the total or the sum of all of these shapes together, 'cause it's balancing and it's showing that we've decomposed or broken apart 48 into all of these different shapes.
[At the top of the page where the speaker has recorded the total amounts of each shapes, she adds a + so that it now reads 5 + 2 + 4 + 5. To the right of that text she writes: sum is 48.]
Speaker
So we could document that here and say that if we added our five triangles, to our two rectangles, to our four trapeziums, to our five hexagons, that the sum is 48. Mathematicians, that's got me thinking. I wonder if we could use all of this information that we've noticed to help us figure out what the value is of each of these individual shapes. Yeah, that sounds like a fun puzzle, doesn't it?
[In the top left corner the speaker draws a trapezium and then a = followed by a _. In red pen she writes rectangle = _. In green pen: hexagon = _. In pink pen: triangle = _.]
Speaker
So we'd want to know what just one trapezium has a value of and what one rectangle has a value of and one hexagon and one triangle. How could we start to figure that out?
[White text on blue: Over to you mathematicians…]
Speaker
So it's over to you as mathematicians, see if you can figure out the value of each individual shape. And when you're ready, watch the next video.
[The NSW Government logo flashes on screen. Text below reads: Copyright, State of New South Wales (Department of Education), 2021.]
[End of transcript]
What to do
Look at this image below and write what you notice.
How could you determine the value of each shape?

Watch
Watch Math mobiles video part 2 (10:41).
[Bold, white text on a blue background: Let’s investigate!. In the bottom right corner is the white waratah logo of the NSW Government. In the bottom left corner in small font text: NSW Mathematics Strategy Professional Learning team (NSWMS PL team)]
Speaker
Welcome back, mathematicians. How did you go? This is one way that I found to solve this puzzle.
[A pair of hands wave. On a table is a large piece of butcher’s paper. In the top left corner is an image of a math mobile with a series of shapes hanging by a series of horizontal lines from the number 48. Above the image is a hand drawn series of shapes and symbols. From left, they are a blue trapezium =_, a red rectangle =_, a green hexagon =_ and a pink triangle =_.
To the right of the image is handwritten text.
Notice? 5 triangles + 2 rectangles + 4 trapeziums + 5 hexagons. Sum is 48. Beside each digit and shape is the word: equivalent.
Below is the text: Lines connecting different shapes showing balance (equivalence).
Below are a series of equations.
2 trapeziums + 2 rectangles + 2 hexagons + 2 triangles = 2 trapeziums + 3 hexagons + 3 triangles
trapezium + 2 hexagons = 3 triangles + hexagon + trapezium
trapezium + rectangle + hexagon + triangle = trapezium + rectangle + triangle + hexagon
trapezium = rectangle + triangle + hexagon
rectangle + triangle = hexagon
trapezium = 2 hexagons
3 triangles + hexagon = trapezium.]
Speaker
Welcome back, mathematicians. How did you go puzzling over this puzzle? it's a bit of a brain sweat, isn't it? I've had lots of fun, and I think I found a way of solving it but I'd love your help. So when I was looking at this, I started to think, well, how can I use all of these relationships that I've seen to help me figure out the value of each of these individual shapes?
[The speaker circles the first equation, 2 trapeziums + 2 rectangles + 2 hexagons + 2 triangles = 2 trapeziums + 3 hexagons + 3 triangles. Each side of the equation corresponds to a half of the mobile. She writes ½ of 48 above each half and draws a dotted line down the middle of the image.]
Speaker
And I was looking at it and wondering where to get started but then I thought that this noticing was really important because this one was showing that this part and this part were equal, equivalent in value. And what that means is that they're equal parts of our whole collection, which is 48. So I knew that I could rename that as this part being half of 48 because two equal parts of a whole are halves and this part is also half of 48 and so I decided that I would begin by looking at just one of those parts. And I saw also that lots of these trapeziums are by themselves, there's two over here.
[Below the right hand half of the mobile she writes number and draws shapes: 2 trapeziums + 3 hexagons + 3 triangles = half of 48 = 24.]
Speaker
And so I thought this might be a good place to start so I can figure out at least one of the shapes. So looking at this, I can write that as saying that we have two trapeziums here, one, two and three hexagons and three triangles and all of those shapes together are equivalent in value to half of 48, which we know we can rename as 24, right, because double 24 is 48. Aha, and then looking at that, I thought, well hang on, there are more of these halving relationships.
[The speaker indicates two sub-branches on the left-hand side of the mobile and writes ¼ of 48 above one of those sections and then 1/8 of 48 below a single strand with one trapezium.]
Speaker
Can you see that because this is half of 48 but then here our shapes get partitioned again into two halves and I know a half of a half is a quarter. So that means that these shapes together must be a quarter of 48. And that means that here where we divide again into two equal parts, this side must be an eighth of 48 and this side must also be an eighth of 48. Yeah, OK.
[She writes: trapezium = eighth of 48. Below that she writes: trapezium = 48/8 = 6.]
Speaker
And so that is really starting to help because I can look at just that trapezium and say that it must be equivalent in value to an eighth of 48. Yeah, and we could rethink that and say that the trapezium is equivalent in value to 48 divided by eight. And I can write that like this or 48 eights, isn't it. And we know that we can rename 48 eighths as six wholes because there are six eighths in 48. And so look at these, we have discovered that the trapezium has a value of six.
[At the top of the paper, she fills in the blank space beside the hand-drawn trapezium so that it reads: trapezium = 6. She writes 6 inside each trapezium on the mobile.]
Speaker
Oh, that's fantastic, let's record that. So our trapezium has a value of six and then we can fill in all of the trapeziums because we've already noticed that they're the same as each other so they must have the same value. Whoa, look at this, our puzzle is starting to come together. Alright, so here we can see that six, the trapezium, is equivalent in value to the two hexagons so let's work on that.
[She draws a line below the equations and writes: 6 = 2 hexagons. Below that she writes 6 = 3x2 and then hexagon = 3.]
Speaker
So six is equivalent in value to two somethings, two hexagons. So I can look at this as being double something is six and that makes it a lot easier because I know that double three is six. Uh-huh, so that must mean that one hexagon has a value of three. Fantastic. Alright, so we've figured that out.
[She fills in the blank beside the hexagon drawing at the top of the paper so that it reads: Hexagon = 3. She writes a 3 on each of the hexagons on the mobile.]
Speaker
So three is our hexagon, and we can fill them in here as well. Three, three, three, three, look at these, it's coming together nicely.
[She indicates the right most two branches of the mobile, which now has only 3 triangles left to solve.]
Speaker
Oh, and this will be a nice one to solve now, because this is showing me that we have, what have we got?
[She writes: 3 triangles + 3 = 6.]
Speaker
So we've got three somethings, three triangles and three has a value of six. Yes and I can see that six is three and something more or I could think about that in subtraction and think that three is three less than six, right? So that must mean that I just need to third my three somethings to figure out what the triangle is. So three somethings and three is six. So three ones, yeah.
[She writes: triangle = 1. She fills in the top equation so that it reads triangle = 1 and then writes the number 1 in all of the empty triangles on the mobile.]
Speaker
So one triangle must be equivalent in value to one. Look at this, so let's check our thinking. So we know that all of these shapes must have a sum of half of 48 or 24. So we've got six and six, double six is 12 and then six and six is 12. So that's 12 and 12 is 24. Aha, we are getting somewhere. Oh OK, over this side we've got this triangle and this triangle. So we also know those values. So let's have a look at, Oh look, all we need to solve on this side now are the rectangles.
[She points to the right hand branch which has 2 unsolved rectangles.]
Speaker
And so I'm looking at that and I'm thinking that this section here might be really helpful for us because I can see a really simple relationship and it's one that we found over here as well, isn't it?
[She circles the equation trapezium = rectangle + triangle + hexagon.]
Speaker
We saw here that the, Oh, no hang on, not that one. It's this one here.
[She circles the equation rectangle+ triangle = hexagon. She writes an equation below the right hand branch: rectangle + triangle = hexagon.]
Speaker
The rectangle and the triangle is equivalent in value to the hexagon. So the rectangle and the triangle is equivalent in value to the hexagon but we now have solved some of these values, haven't we, and we know some of them.
[She writes: rectangle + 1 = 3.]
Speaker
So we're actually just saying that something and one is equivalent in value to three and that's really simple, isn't it, because one is just two less than three.
[She writes: rectangle = 2. She writes 2 in both of the rectangles on the mobile and fills in the top equation so that it reads rectangle = 2.]
Speaker
So our rectangle must be equivalent in value to two, two and one is 3. Two, two, let's check our thinking. So we've got three and three, so double is six and six is 12. Uh huh and another 12 is 24, 24 and 24 is 48. Look at that mathematicians, we've solve our puzzle. You might have found a different way to solve this puzzle, did you? Yeah, or maybe you could investigate a different way now. It's so great as mathematicians because we can look at the same problem in lots of different ways.
[White text on blue: Over to you mathematicians… Can you find a different way of solving this puzzle? Then, try solving the next 2 puzziles on your own, with your friends, family or classmates…]
Speaker
So it's over to you mathematicians. Can you find a different way of solving this puzzle? And then try solving the next two puzzles on your own with your friends, family or classmates. Are you ready? Here we go.
[New slide. Text: What do you notice?...
An image of a math mobile.
The top number is 60 and horizontal lines separate in to 2 branches. Both the left and the right branch are separated into 2 sub-branches.
On the left, the left most line has a series of 5 shapes. From the top they are a red hexagon, a green square and 3 blue triangles. The other half of the branch has three separate lines, with just one shape on each. From left they are a red hexagon, a blue triangle and a red hexagon.
The right-hand branch has 2 lines. The left line has 3 green squares, and the right line has 2 red hexagons and a blue triangle.]
Speaker
Yes, it's very tricky, isn't it?
[New slide. Another math mobile.
The top number is 80 and it is split into 2 branches. The left branch has 2 sub-branches. The leftmost sub-branch has a line of 2 pentagons and 1 green rectangle. The right sub-branch has a line of a pink triangle and red circle and a line of 2 blue pentagons.
The right-hand branch has a green rectangle on a line before the branch split into two lines. One line has a red circle, a blue pentagon and a pink triangle. The other line has 3 pentagons.]
Speaker
Have a look at this one. Oh, I think it's going to be a brain sweat. Have fun, mathematicians.
[New slide. Text: What’s (some of) the mathematics?]
Speaker
But just before you go, let's have a look at what some of the mathematics is.
[New slide: Text: Equivalence can sometimes be described as balance.
Below the text is an image of the math mobile which the speaker worked on.
A red circle appears over the left-hand branch with 2 trapeziums, 2 rectangles, 2 hexagons and 2 triangles.
An = divides the two halves.
A circle appears over the right-hand branch which has 2 trapeziums, 3 hexagons and 3 triangles.]
Speaker
Equivalence can sometimes be described as balance and we can see that really clearly in this diagram where we saw that two trapeziums, two rectangles, two hexagons and two triangles were equivalent in value to two trapeziums three hexagons and three triangles. We saw these equivalent or balanced relationships everywhere we looked.
[A yellow oval appears over the leftmost line of shapes, a trapezium, rectangle, hexagon and triangle.
An = appears beside that line of shapes.
A yellow circle appears over the 3 lines to the right of the branch, which has a trapezium, rectangle, triangle and hexagon.
Blue circles and a = appear over the two halves of the right hand branch.
Green, pink, blue and orange circles appear over the other 4 set of halves.]
Speaker
We saw that the trapezium, rectangle, hexagon and triangle together were equivalent in value to the trapezium rectangle, triangle and hexagon. We also saw equivalence here and here and here and here and even here.
[New slide. Text: Numbers can be partitioned (broken apart/decomposed) in different ways.
- When you decompose a number in different ways, the total remains the same but the parts we break it into can look really different (for examples when we halve 48, it looks and sounds different to quartering or even eigthing 48, but there’s still 48 in total).
A red line divides the mobile into halves. Text: 1-half, appears above each half. Text: 1-quarter, appears above each quarter. Text: 1-eigth, appears above one of the eighth sections.]
SPEAKERS:
Numbers can be partitioned or broken apart, decomposed in different ways. When you decompose a number in different ways, the total remains the same but the parts we break it into can look really different.
[New slide. Text: As mathematicians we can records our thinking using symbols and diagrams. This helps us to see relationships between numbers. For example, more and less, halves, quarters and part-part-whole relationships.]
Speaker
For example, when we half 48, it looks and sounds different to quartering or even eighthing 48 but there's still 48 in total. As mathematicians, we can record our thinking using symbols and diagrams. This helps us to see relationships between numbers. For example, more and less, halves, quarters and part part whole relationships.
[A red circle appears of the right half of the mobile. An image appears of a handwritten equation: 2 trapeziums + 3 hexagons + 3 triangles = half of 48 = 24.]
Speaker
This was particularly useful when we were looking at this part of the diagram where we could see that two trapeziums and three hexagons and three triangles were equivalent in value to half of 48, which we knew we could rename as 24.
[An image of handwritten equations: trapezium = eighth of 48. Trapezium = 48/8 = 6.]
Speaker
We then realised that to figure out the value of our trapezium, all we needed to do was find eighth of 48 because we were halving, halving again and halving again. And then we realised that 48 divided by eight or 48 eighths is equivalent in value to six.
[An image of a handwritten equation: 6 = 2 hexagons. 6 = 3x2. Hexagon = 3.]
Speaker
So six was equivalent in value to two hexagons. So one hexagon must have been three.
[The NSW Government logo flashes on screen. Text below reads: Copyright, State of New South Wales (Department of Education), 2021.]
[End of transcript]
What to do
- Solve the 60 and or 80 math mobile.
- Investigate if there is more than one way to solve the 60 and 80 math mobile.
Discuss
Make your own math mobile and challenge a friend, family member or classmate to solve it!