Math mobiles – Stage 2
A thinking mathematically targeted teaching opportunity focused on investigating unknown values using equivalence.
Adapted from a task by Boaler, J., Munson, J., & Williams, C. (2019). Mindset Mathematics: Visualizing and Investigating Big Ideas, Grade 6 (1st ed.). Jossey-Bass
Images reproduced with permission of John Wiley & Sons, Inc.
Syllabus
Syllabus outcomes and content descriptors from Mathematics K–10 Syllabus © NSW Education Standards Authority (NESA) for and on behalf of the Crown in right of the State of New South Wales, 2023
Outcomes
- MAO-WM-01
- MA2-AR-01
- MA2-AR-02
- MA2-MR-01
- MA2-MR-02
Watch
Watch Math mobiles video part 1 (8:27) to see what to do. What do you notice about the mobile?
This video was created with Sarah from Newtown PS.
Speaker
Hi there, mathematicians. Welcome to Maths Mobiles. These puzzles come from Boaler, Munson and Williams.
For today, you're going to need something to write on and something to write with.
All right, mathematicians, it's time to get our brains sweaty with a great puzzle. Are you ready? Okay. What do you notice in this image?
[Screen shows a maths mobile that begins with the number 16. It splits into 2 lines. The lines on the right side split into 1 star and 2 hexagons. The lines on the right side first split into a star and then branches further into 2 triangles and a hexagon.
Screen reads: What do you notice?]
Ah! Yes. It's really interesting, isn't it?
Okay, press pause and write down everything you're noticing and then press play and we'll investigate.
[Screen reads: Let’s investigate!]
Welcome back, mathematicians. How did you go with your noticing? Yeah, I bet you've noticed some really interesting relationships in this image. Yeah, me too. Shall we record our thinking? Yeah, because we know that mathematicians like to record their thinking because it makes it easier to see patterns and relationships.
[Speaker writes the heading ‘Notice?’ at the top of the page.]
So what was the first thing we noticed? Ah! Yes. I also noticed straight away, that there were lots of different types of shapes in this image. Yeah, and we could sort of sort the shapes, couldn't we? Because we've got 2 of these stars and they're blue. And then we've got one, 2, 3, 3 of these green shapes. What should we call these green shapes? Yes. Okay. So there's one, 2, 3, 4, 5 6 sides and that means 6 angles, so we know we can call this shape a hexagon because hex means 6, doesn't it?
[Speaker writes: 2 stars, 3 hexagons and 2 triangles.]
Yeah, and these ones are green. It's quite a long hexagon, isn't it? Okay. Yes, and then we've got these 2 triangles. And they're pink, aren't they? Ah, yes, that's right! Some of you are noticing that each of the shapes that are the same are actually the same. So if we look at the stars, they're exactly the same size. And shape and colour, yeah, you're right. And colour as each other. Oh, yeah, and it's the same for the hexagons, isn't it? So they're exactly the same. So, oh! We could actually say that they are equivalent to each other because that just means the same as. Yeah, and it's the same as the triangles. They're also equivalent, aren't they? They're exactly the same.
[Next to the words ‘2 stars’, speaker writes ‘same size, shape, colour as each other. Next to 3 hexagons and 2 triangles she writes the word ‘equivalent’.]
Okay, what else did you notice? Yeah, I was wondering about these lines, too. Yeah, the whole image sort of looks like it's a mobile, doesn't it? Like it would, if I held it up, it would balance perfectly.
So these lines are connecting are connecting some of the shapes.
[Speaker writes: lines are connecting shapes and they are balanced like a mobile.]
And yeah, because these lines are straight, it sort of shows that they're balanced, doesn't it? So it must mean that whatever's on one side of that straight line is the same weight as the other side. So how could we write that?
Lines connecting shapes and ah, yeah, they are balanced like a mobile. Yeah, interesting. We haven't talked about this yet, have we?
So there's this big circle at the top, and it's got a 16 in it. And I was wondering about that, too. What could that mean? Ah! Yes. Yes, you're right.
So that's 16 with all these shapes underneath balancing must mean that when we combine all of these shapes, they have a total of 16. Yeah, so, we could write that like 16 is the sum of, so when we add them all together, we'll get this sum of all of our shapes.
[Speaker writes: 16 is the sum of a triangle and triangle and hexagon and hexagon and hexagon and star and star.]
So a triangle and another triangle and oh, I'm going to need to go down, aren't I? A hexagon and a second hexagon and a third hexagon. And yeah, the 2 stars. Star and the star. Wow. Isn't that cool? So 16 is the sum of all of these shapes together.
Oh, looking at that, I think we could rewrite that in a different way. Think about it a bit differently. We could say that 16 is equivalent in value equals 2 of these triangles and uh-huh, 3 of these hexagons and 2 of our stars.
[Speaker rewrites the sum as: 16 equals 2 triangles and 3 hexagons and 2 stars.]
Wow. Look at that.
Oh, yes! Some of you are also noticing something about this 16 and the lines. Yeah. Because here, if we follow this line down here and then across, it looks like our 16 is being divided or partitioned into 2 parts. So 16 is being partitioned into 2 parts.
[Speaker writes: 16 is being partitioned into 2 parts that are equal (halves).]
Ah, yes! And yeah, you're noticing that too, that because this line is straight and it's balanced, each of these parts must be equal to each other.
So it's been partitioned into 2 parts that are equal. Uh-huh. Ah, yes! And we know that when we have 2 parts of a whole that are equal, we can rename them as halves, can't we? Yeah! So we've got one part here and that must be 1/2 of the 16. And then we've got another part. Look here. And that must also be another half of the 16.
Mathematicians, this has got me wondering. I wonder if we could use this information and everything we've noticed to figure out what the value is of each of our shapes.
Yeah. Because we know that they all add up together to create 16. So we should be able to figure out what the value is of one star and what the value of one hexagon is, and what the value of the triangle is.
[Speaker writes: Star equals blank, hexagon equals blank and triangle equals blank above the Maths mobile.]
Yeah, okay. Let's give it a go.
Can you help?
All right, so I might draw a dividing line just to help us organise our thinking. How should we start?
[Speaker draws a dividing line, dividing the maths mobile into 2 parts.]
Pause the video now and see if you can figure out a way to try to solve this.
So it's over to you, mathematicians. See if you can figure out the value of each individual shape. And when you're ready, watch the next video.
What to do
Look at the image below and write what you notice.
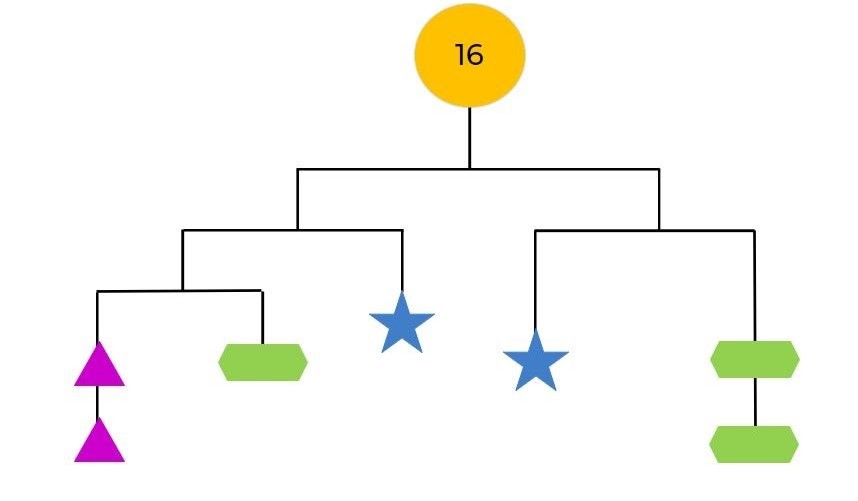

See if you can find the value of each shape and solve this math mobile.
Watch
Watch Math mobiles video part 2 (9:13) to see what to do next. Investigate the value of symbols using equivalence.
Speaker
Welcome back, mathematicians. How did you go?
This is one way that I found to solve this puzzle. Yes, I also thought that, that we should maybe start on this half, because it looks a little bit simpler to deal with, doesn't it?
Yeah, let's do that. All right.
[Speaker points to the right side of the Maths Mobiles puzzle.]
So we know that this part is half of 16 and... Oh, okay, so we could say that the star and the 2 hexagons combined together are equivalent in value to... Yeah, half of 16, right?
[Speaker draws the equation as she speaks. She draws star plus hexagon plus hexagon equals half of 16.]
Yeah, great.
And ah, yes, some of you are noticing this, that if we follow this line down, it's divided into 2 parts, and they're balanced, aren't they? So this star must be half of the half of 16.
[She writes another equation. It says star equals half of the half of 16.]
Yes, so the star... Oh, hold on. The star is equivalent in value to half of the half of 16. Yeah. Oh, yes. And we actually know something more about this, don't we? Because half of 16 is equivalent in value to 8, right? Because double 8 is 16.
So, if the star and the 2 hexagons is equivalent to 8 and the star is half of the half of 16... Oh, okay. So we could think of that as also being the same as a quarter of 16, uh-huh. Yes, so half of 16 is 8, and half of 8 is 4. Yes, so the star has a value of 4. Fantastic.
[She adds equals a quarter of 16 underneath. She then writes star equals 4.]
All right, we are solving this puzzle.
So we've figured out that the star is equivalent in value to 4. And oh, yes, we know that the star is equivalent to the 2 hexagons together, don't we? Because they're balanced. So how could we use that to help us figure out what just one of the hexagons' value is? and that's the same as 2 of those hexagons.
[She then writes a new equation which is a star equals 2 hexagons. Underneath she writes 4 equals a hexagon plus a hexagon.]
So that must mean that just one... Oh, that was a bit of a wonky one, wasn't it? That just one of these hexagons must be half of 4. Yes, and that makes it much simpler, doesn't it? Because we know that half of 4 is 2. Ah, so we've figured out the value of 2.
[She writes hexagon equals 2.]
We better just check our thinking to make sure. So if the hexagons are worth 2 each and the star has a value of 4, then, when we add these up, 4 and 4, so double 4 is 8 and 8 is half of 16.
[She writes the number in each shape and adds them together to find 16.]
Yes, so it's working. All right, let's use what we've figured out here to help us on this side. So we know that our star has a value of 4, and it's exactly the same, so we don't even need to check that, and that our hexagon has a value of 2. Uh-huh, so... Oh, yes, and we know that this part is half of 16, so we could say that our 2 triangles with our hexagon and our star has equivalent value of half of 16, which we already know is 8, don't we?
[She writes a new equation on the left side. She writes triangle plus triangle plus hexagon plus star equals 8.]
Oh, yes, but we know more about this, don't we? Because we don't know what the value of these triangles is yet, but we do know that the hexagon is 2 and the star is 4. So let's have a look at this equation.
[Underneath her first equation she writes triangle plus triangle plus 2 plus 4 equals 8.]
Triangle and triangle and 2 and 4 is equivalent in value to 8. Sounds quite cool, doesn't it? So, hmm, all right. How could I think about this? Well, I know that 2 and 4 is 6, so this must be saying that something and something and 6 is 8.
Ah, yes. Yes, I see that too. We know that 6 is 2 less than 8, which must mean that our 2 triangles, when they're combined, give us a value of 2. 2 and 2 is 4 and 4 more is 8. Ah, yes, and because they're the same, they have to be the same value, don't they? So there's only one possibility. Half of 2 is 1. So one triangle has a value of 1.
[She writes triangle plus triangle equals 2. She writes triangle equals 1.]
Let's check our thinking. All right, 1 and 1 is 2. Double 2 is 4. Double 4 is 8 which is half of 16. So if we added our 2 parts, 8 and 8 we have 16.
Mathematicians, we have solved this incredibly brain sweaty puzzle.
You might have come up with a different way of solving this as well. Did you? Uh-huh, isn't it great that as mathematicians, we can look at the same problem in lots of different ways?
So it's over to you, mathematicians. Can you find a different way of solving this puzzle, and then try solving the next puzzle with your friends, family, or classmates?
Are you ready? Uh-huh, yes.
This is going to be a real brain sweat, isn't it? Have fun, mathematicians.
But before you go, mathematicians, what's some of the mathematics? We've learnt that equivalence can sometimes be described as balance, and that was showing really clearly on our diagram, which looked like a balancing mobile.
From this, we could tell that 16 was the total, or the sum, of all of our shapes combined because of the way that it balanced. We also noticed that 16 is being partitioned into 2 parts that are equal, or halves. And another way that we could talk about this is that the 2 triangles, the hexagon, and the star are equivalent in value to the star and the 2 hexagons.
We also noticed that the star was equivalent in value to the 2 hexagons. You might have noticed some other relationships as well. You could see that the 2 triangles and the hexagon were equivalent in value to the star and that the 2 triangles were equivalent in value to the hexagon.
Numbers can be partitioned, or broken apart, or decomposed in different ways. When you decompose a number in different ways, the total remains the same, but the parts we break it into can look really different. For example, when we have 16, it looks and sounds different to quartering 16, but there's still 16 in total.
As mathematicians, we can record our thinking using symbols and diagrams, and this helps us to see relationships between numbers, for example, more and less, halves, quarters, and part-part-whole relationships. We saw that especially today when we were looking at this part of our diagram and we were trying to figure out the value of the 2 triangles. We figured out that a triangle and a triangle and 2 and four was equivalent in value to 8, or half of 16. And from that, we saw that 6 is 2 less than 8. And so we realised that the 2 triangles must be equivalent to 2.
When we asked ourselves, "Double something is equivalent in value to 2," we realised that we needed to halve, and so we figured out that one triangle had a value of 1.
What to do
Can you find another way to solve the 16 math mobile?
Solve the math mobile below on your own, or with your friends, family or classmates.
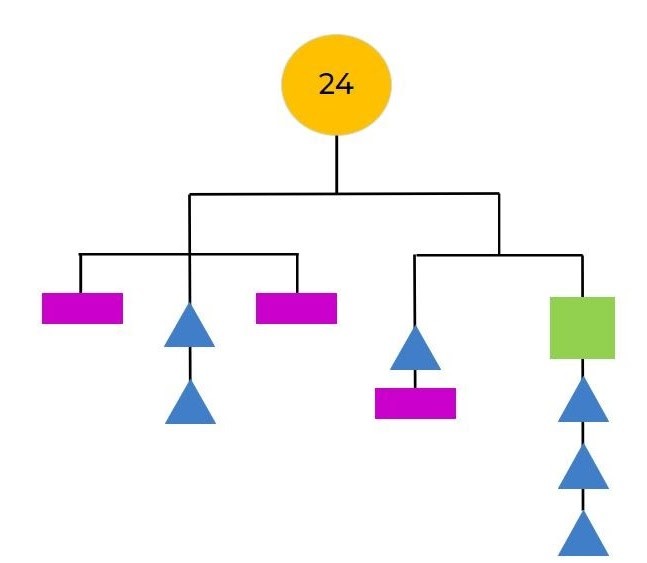

Discuss
Make your own math mobile and challenge a friend, family member or classmate to solve it.