Raindrops
Stage 3 – A thinking mathematically context for practise exploring different ways to visualise and represent growing and shrinking patterns
Adapted from youcubed
Syllabus
Syllabus outcomes and content descriptors from Mathematics K–10 Syllabus © NSW Education Standards Authority (NESA) for and on behalf of the Crown in right of the State of New South Wales, 2023
Outcomes
- MAO-WM-01
- MA3-MR-02
Collect resources
You will need:
pencils/ markers
your mathematics workbook.
Instructions
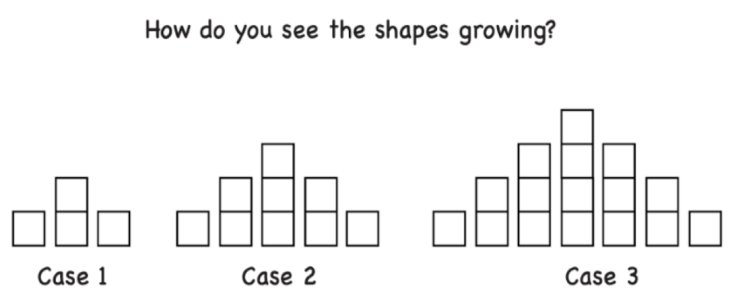
What do you notice when you see this image?

Watch
Watch the Raindrops video for 3 different ways of thinking (3:33).
[A slip of paper is laid out over a white surface. On it, are 3 groups of pyramid shapes, all made from small squares. Each pyramid is bigger than the previous one. The first group is labelled “Case 1”. It features a rectangle in the middle, which is made from 2 stacked squares, with 2 individual squares either side of it. The second group is labelled “Case 2”. It consists of a middle rectangle, made from 3 squares. Either side of that is a shorter rectangle, made from 2 squares. On the outer sides of the pyramid, are 2 individual squares. The central rectangle of the final pyramid is made from 4 squares. The rectangles either side of that consist of 3 squares, then 2 squares, then one square.]
Speaker:
Alrighty, everybody. I'm joined here today by two of my favourite mathematicians, Barbara and Aisha. Hi, guys.
Barbara:
Hi.
Aisha:
Good morning.
Speaker:
All right. Are you ready to get started?
Barbara:
Yes.
Speaker:
So we're looking at a problem today, which is asking us about how the shapes or the squares are growing. And so case one... Sometimes we refer to the case as the term in a pattern. So case one, case two, and case three. And what I'm interested in, where do you see the growth happening?
Barbara:
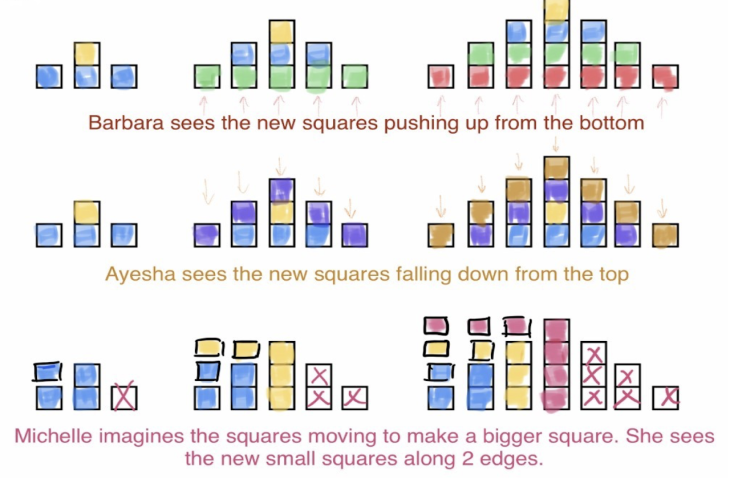
Oh, OK. Well, I think for me, it's like there's another bottom road coming in each time.
[Barbara points along the bottom of the shape labelled “Case 1”.]
Barbara:
So if you look at case one there, if we add another one on the bottom here and there and there and there and there, it looks like case two.
Speaker:
So, I'm gonna use this post-it notes to try to model that sort of idea, alright?
[The speaker lays down a row of 3 blue squares of paper. She places a yellow square if paper above the blue square in the middle. It matches the shape labelled “Case 1”.]
Speaker:
So if I make case... This, like this one. Which is case one. And so you're saying then what happens for you is the next case comes in underneath?
[The speaker lays a row of 5 brown squares of paper beneath the row of blue squares. The arrangement of coloured squares now matches the shape labelled “Case 2”.]
Barbara:
Yeah. That's right. And then in case three, there'll be another row added to the bottom.
Speaker:
And it's also almost like...
[The speaker places one purple square below and to the left of the row of brown squares.]
Barbara:
But it will be wider. It'll start...
Speaker:
Yeah, right. Like this and it would start to shift up.
Barbara:
Exactly right.
[The speaker removes the purple and brown squares, leaving the row of 3 blue squares and one yellow square.]
Speaker:
What about you Aish? How do you see it?
Aisha:
I'm quite the opposite to Barbara, actually. So for case one, I see that instead there are squares falling down like raindrops to create case two.
[Aisha uses her finger to mime raindrops falling down over the squares in the shape labelled “Case 1”. The speaker moves the coloured squares of paper down.]
Speaker:
So if I move this down a little bit more. So case one stays the same. Everybody sort of has that.
[The speaker adds 5 brown squares to the arrangement, one on either side of the bottom row, and then one on top of each existing column. The arrangement of coloured squares now matches the shape labelled “Case 2”.]
Speaker:
And then you're saying that for you in your head, what happens is these come in like raindrops and fall down.
Aisha:
That's right.
Speaker:
And rest on top of a square that already exists.
Barbara:
Oh, wow, that's really different to what I was thinking.
Aisha:
Yeah.
Speaker:
What are you thinking?
[The speaker removes the brown squares of paper.]
Aisha:
Well, I think about it differently again. So I sort of in my head, rearrange things.
[The speaker points to the remaining coloured squares, arranged to match the shape labelled “Case 1”. She takes the square on the right and moves it above the square on the left. The coloured squares are now arranged into a larger 2 by 2 square.]
Aisha:
So if this is case one, what I imagine is this square here moving across, and I reposition it in my head so now I can see a square.
[The speaker lays the brown squares over the top of the larger square, and down the right-hand side. The coloured squares are now arranged into a larger 3 by 3 square. The speaker moves the 2 coloured squares in the top corners of the overall arrangement, and lays them down on either side so that the arrangement of coloured squares now matches the shape labelled “Case 2”.]
Aisha:
And when the new ones come, they come across the top row. And then down the side. So if I reorganise it, you'll still see the same structure as case two.
Barbara:
Oh, but you're noticing that it squares every time.
[The speaker removes the brown squares and puts the blue and yellow squares into their original arrangement; 3 blue squares on the bottom row and one yellow on top. She then tops each row with a brown square, and places 2 brown squares on either side so that the overall arrangement matches the shape labelled “Case 2”.]
Speaker:
Yeah. So I'll show you the same squares. So this comes to here, and if I use Aisha's method, for example. Like this. But what happens in my head each time is I can see that that would form this triangular piece, and I rotate it around in my head so that it come over to here like this.
[The speaker rearranges the coloured squares of paper into a larger 3 by 3 square.]
Barbara:
That's even more different to how I was thinking.
Speaker:
I wonder who else has some different ways to think about, you know, how do they see the growth occurring in the pattern? And then can you use that to help you work out what would the fourth case look like? Or the 10th case? For example. Over to you mathematicians!
[Over a grey background, the red waratah of the NSW Government logo appears amongst red, white and blue circles. Text: Copyright State of New South Wales (Department of Education), 2021.]
[End of transcript]
Discussion
You might have noticed things like:
In case 2 there are more cubes than in case 1.
In case 3 there are more cubes again.
Where do you see the extra cubes adding each time?
There are many ways to answer this question as people see the cases in lots of different ways. How do others see them?

Share/Submit
Share your work with your class on your digital platform. You may like to:
- share your discoveries
- write comments
- share pictures of your work
- comment on the work of others.