Max's toothpick problem
A thinking mathematically targeted teaching opportunity exploring different strategies to quantify a collection of objects by looking and thinking
Adapted from a task by Dianne Siemon
Syllabus
Syllabus outcomes and content descriptors from Mathematics K–10 Syllabus © NSW Education Standards Authority (NESA) for and on behalf of the Crown in right of the State of New South Wales, 2023
Outcomes
- MAO-WM-01
- MA3-MR-01
- MA3-MR-02
Collect resources
You will need:
something to write on
something to write with
some toothpicks, straws or paper strips.
Watch
Watch the video and think about how you would solve Max's toothpick problem (12:22).
[White text over a navy blue background: Max’s toothpick problem. Adapted from Professor Dianne Siemon. In the lower right-hand corner is a red waratah logo of the NSW Government. In small font in the lower left-hand corner is the text: NSW Mathematics Strategy Professional Learning team (NSWMS PL team).]
Speaker
Hi mathematicians. Welcome back. Today we're going to explore Max's toothpick problem. And this problem was shared with us from Professor Dianne Siemon. And Professor Di is a brilliant mathematician and we always love solving her problems.
[New slide: You will need…
- Something to write on
- Something to write with
- Some toothpicks, straws or paper strips.]
Speaker
You will need something to write on, something to write with, and some toothpicks, or you could use paper straws or small paper strips to represent our toothpicks.
[New slide: Let’s investigate!]
Let's investigate.
[New slide: Max’s toothpick problem. Adapted from Professor Dianne Siemon.
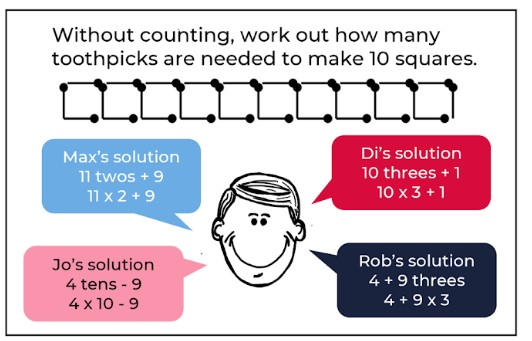
Inside an outlined square is the text: Without counting, work out how many toothpicks are needed to make 10 squares.
Below the text is an image of 10 squares in a horizontal row. Each square is made of four toothpick-like lines, with the toothpick that makes up the right edge also acting as the left-hand edge of the next square in line.
Below the line of squares is a drawing of a face with four speech bubbles surrounding it.
The top left speech bubble says: Max’s solution. 11 twos + 9. 11 x 2 + 9.
The bottom left speech bubble says: Jo’s solution 4 tens – 9. 4 x 10 – 9.
The top right speech bubble says: Di’ solution 10 threes + 1. 10 x 2 + 1
The bottom right speech bubble says: Rob’s solution 4 + 9 threes. 4 + 9 x 3.
To the right of speech bubbles is the text:
- Do each of these strategies work?
- Explain each persons thinking.]
Speaker
And our problem today is this, without counting, can you work out how many toothpicks are needed to make ten squares? And you can see on the page here that we have four different strategies from Max and his friends. And what we need to do is think about do each of these strategies work? And also try and explain each person's thinking. Over to you.
[On a table is a sheet of paper with a hand-drawn example of the 10 toothpick squares and each of the potential solutions.
In the top left is the text: Di. 10 threes + 1.
In the bottom left: Jo. 4 tens + 9.
In the top right: Max. 11 twos + 9.
In the bottom right Rob 4 + 9 threes.
Also on the table are two piles of small strips of paper, coloured blue and green.]
Speaker
Hi there mathematicians. Welcome back. How did you go? Were you able to determine that we'd need 31 toothpicks in order to create and form our pattern of ten squares? And so let's get started with Max. We can tell and we know that Max saw our pattern here of ten squares by 11 two's and nine more.
And that got me thinking about, well, what are the twos that Max attended to? If we take two of our toothpicks here, I'm using little strips of paper instead of toothpicks, we can start to think about what are these twos Max attended to?
[The lecturer places two green strips of paper in an L-shape – making the bottom and left edges of a square.]
Speaker
So it could be the two of the L, like this.
[She places the strips beside one another with a space in the middle, as if making the left and right edges of a square.]
Speaker
He may have also saw the two as the first and the first internal toothpick to see his twos. So I'm thinking perhaps Max attended to the top and the bottom as two.
[She swivels the paper around so that they form the top and bottom edges of a square.]
Speaker
So if that's how Max saw the first two, he could use this in knowing that will actually I know I need ten of them to make the top and bottom row, and one more two, one and one, could be used to close off either end of the pattern. So let's see if that works. We have two... You know what, actually I might tape those together just to make them a little bit easier.
[She sticks the two strips together with sticky tape.]
Speaker
We have our one, two. And now we need 11 twos. So we have one, two and I have a few here that I prepared a little earlier to help us show Max's thinking.
[The lecturer places the stuck together pieces of paper beside one another until she has lined up ten lots of two strips of paper connected by sticky tape. This has made ten top edges and ten bottom edges.]
Speaker
So we have one two, two two's, five two's, six twos, seven two's, eight twos. So we have eight twos so far, nine twos and ten two's.
[She adds a loose strip of paper to the far left edge and far right edge of the line of squares.]
Speaker
And we now need our two... Or this two to form and close off the pattern. He's falling off the edge there but you can see. So we have our 11 twos. And I can already see that the nine that Max has written here, the +9, must be the nine internal toothpicks. And it actually shows us that each of our squares shares a bordering toothpick in order to form the square. So we have 11 twos.
[The lecturer adds 9 blue strips of paper to form squares out of the existing shape.]
Speaker
We have our eleven twos, we have our one two and our ten twos and nine more. And 11 twos we know is 22, plus nine more is total of 31. So Max also found that we needed to have 31 toothpicks in order to create our ten squares.
[The sheet of paper is cleared.]
Speaker
Let's dig into Di's thinking now. We know that Di saw this pattern as ten threes and one more. But what we need to do is to think about how Di saw the problem. And this is where as a mathematician we can use what we notice to then help us solve problems. And if we look at our first square here, we can actually see that each square requires three toothpicks.
So I think when Di thought about this problem, she had her... We have three toothpicks here.
[The lecturer uses the blue strips of paper to form the left, bottom and top edges of a square.]
Speaker
And instead of seeing them as one and two and three to form part of the square, we know that Di actually saw this as one three. And to show that we can actually tape these together.
[She tapes the 3 strips of paper together, connecting the top, bottom and left edges.]
Speaker
Because Di attended to that first three she was to use her knowledge that there are ten squares in order to know that she would need ten threes. So if we were to actually create this using our toothpicks, and I have some that stuck together earlier, we could see that as soon as we start placing our threes down onto our page to form our pattern that each toothpick at the end of our three helps us form that square.
[She places 9 more pieces of paper down each consisting of 3 strips which form the top, bottom and left edges of a square. By placing them side by side, the left edge becomes the right edge of the existing square.]
Speaker
So we have our 10 threes. But I think this is where it's actually becoming noticeable, where the +1 came from in Di's thinking because we still need one more toothpick to close off our square pattern.
[The lecturer adds one loose green strip of paper to form the far-right edge of the pattern.]
Speaker
So we can see Di's thinking of ten threes and one more shown here. And we know that ten threes is 30 and one more makes 31 toothpicks needed.
[The sheet of paper is cleared.]
Speaker
I was just looking at the strategy Rob used to solve how many toothpicks would be needed. And I noticed that he also attended to that idea of threes. That got me thinking about could we use the similar structure that we did with Di to determine if Rob's thinking also works. In Rob's thinking, he saw four first. So I think what he attended to was that first square of our patterns was structured using four toothpicks.
[The lecturer uses 4 loose green strips of paper to make a square.]
Speaker
So we have our four toothpicks there. And I think what Rob did then was attended to, just like Di did, that idea that each of the following squares in the pattern only required three toothpicks in order to form the square. And so if we take our threes or our one three from before, we can start to place those next to our four individual toothpicks.
[The lecturer uses the blue pieces of paper stuck together as she did for Di’s example, except this time she has flipped the paper so that the blue strips form the top, bottom and right edge.]
Speaker
And we can see that we have four and nine three more or 4+27, and we know that 4+27 is also 31. So yes, Rob's strategy of four and nine threes also works to solve this problem.
[The sheet of paper is cleared.]
Speaker
And that brings us to Jo's strategy, which is the last of the thinking we need to dig into. And so if we think about where Jo may have gotten that idea of ten, we know that it's because we have ten boxes in our pattern. But where four? And what I think is Jo thought about each of the boxes as having four toothpicks.
[The lecturer uses four loose strips of blue paper to create a square.]
Speaker
So for each box we have four toothpicks. We know we need another nine boxes all with four toothpicks as well. And so I have some here that I stuck together earlier.
[The lecturer has pre-made squares made of four strips of blue paper stuck together. She places them beside each other.]
Speaker
We have here ten squares, and each square has four toothpicks. But we know Jo then subtracted nine to get to the total of 31. And I think the way she did that was by removing one of the shared... Move that one out of the way, it's that one there.
[The lecturer removes the right edge of the first square she created.]
Speaker
By removing the nine shared toothpicks that each of our squares need.
[The lecturer moves a completed square to the left so that the left edge of the completed square becomes the new right edge of the original square.]
Speaker
So we have... Jumped out of the way. This that then moves over. And we can see that actually yes, that's the start of our pattern here.
[The lecturer moves each of the completed squares over so that a left edge covers a right edge.]
Speaker
And if we continue to cover one to show that we're removing it from our thinking, and we do that nine times or for the remaining nine squares, we can see that actually Jo's thinking also works.
So initially she's thought of the four tens or the ten squares each with four toothpicks separately. And then she thought about how each of the squares had an adjoining toothpick. So she was able to remove nine of those centre toothpicks in order to determine that we need 31 toothpicks to create our ten squares in our pattern.
[White text on blue background: What’s (some of) the mathematics?]
Speaker
What's some of the mathematics?
[Text: We can see and think about the same problem in many different ways.]
Speaker
We can see and think about the same problem in many different ways. For Max's toothpick problem, we were able to dig into the thinking of Di, Max, Jo and Rob to see how they saw the same problem actually really differently yet they still had the same solution of 31 matchsticks are needed to create our ten squares in our pattern.
[New slide. Text: Over to you…
Below the text is a smaller version of the image describing the problem.
The image is of 10 squares in a horizontal row. Each square is made of four toothpick-like lines, with the toothpick that makes up the right edge also acting as the left-hand edge of the next square in line.
Below the line of squares is a drawing of a face with four speech bubbles surrounding it.
The top left speech bubble says: Max’s solution. 11 twos + 9. 11 x 2 + 9.
The bottom left speech bubble says: Jo’s solution 4 tens – 9. 4 x 10 – 9.
The top right speech bubble says: Di’ solution 10 threes + 1. 10 x 2 + 1
The bottom right speech bubble says: Rob’s solution 4 + 9 threes. 4 + 9 x 3.
To the right of the images is the text: Use each strategy we explored today to work out how many toothpicks are needed to make 23 squares.]
Speaker
So over to you mathematicians. Can you use each of the strategies we explored today to work out how many toothpicks are needed to make 23 squares? Have fun exploring.
[The NSW Government logo flashes on screen. Text below reads: Copyright, State of New South Wales (Department of Education), 2021.]
[End of transcript]
Instructions
Without counting , work out how many toothpicks are needed to make 10 squares?
Do each of these strategies work?
Explain each persons thinking.

Discuss and reflect
Use each strategy we explored today to work out how many toothpicks are needed to make 23 squares.