Mathematic-tac-toe
Stage 3 – A thinking mathematically context for practise focussed on building flexible additive strategies and reasoning
Syllabus
Syllabus outcomes and content descriptors from Mathematics K–10 Syllabus © NSW Education Standards Authority (NESA) for and on behalf of the Crown in right of the State of New South Wales, 2023
Outcomes
- MAO-WM-01
- MA3-AR-01
Collect resources
You will need:
paper
2 coloured markers.
Watch
Watch the Mathematic-tac-toe video (4:49).
[White text over a navy-blue background: Mathematic-tac-toe (A mathematical kind of noughts and crosses). In the lower right-hand corner is a red waratah logo of the NSW Government. In small font in the lower left-hand corner is the text: NSW Mathematics Strategy Professional Learning team (NSWMS PL team).
New slide. Text: You will need…
· 2 different coloured markers
· Someone to play with (we love playing this game in teams of two when we can)
· A gameboard
To the right of the text is a picture of a sheet of paper with a hand drawn tic-tac-toe grid. The grid is made of two parallel vertical lines intersecting with two parallel horizontal lines to create 9 boxes.]
Speaker
OK mathematicians. To play Mathematic-Tac-Toe, you'll need two different coloured markers, someone to play with. We love playing this game in teams of two when we can. So it's two versus two. And you'll need a game board. You can see what that looks like here.
[New slide. Text: Let’s play!]
Speaker
Alright, let's play.
[A pile of A4 white paper on a table. Beside the paper are 4 coloured markers. Eddy has a black marker. He draws a tic-tac-toe grid on the top sheet of paper.]
Eddy
I learnt from a teacher named Andrew Lorimer-Derham and he taught me this game that I think he actually may potentially have invented, but it's so delightfully simple that I have to imagine, it has been invented or reinvented many times over throughout time. It's called Mathematic-Tac-Toe, which is a really terrible dad joke, but I'll run with that. So it's just like regular Tic-Tac-Toe, noughts and crosses, with a few crucial differences. So the part that's the same is there's a board, and, you know, columns and rows and diagonals are also part of the goal. But unlike in regular noughts and crosses where we take turns and you put in noughts, I put in crosses, whatever, we're gonna place the digits one to nine. We can only use the digit one side and we can use them only once. So eventually we're gonna use all of them. And there's a goal for one player who's the attacker, and there's a different goal for the other player who's the defender. So I've never explained this game to you, Michelle, so we'll see how you go.
But therefore, I'll let you have the choice. Would you like to be an attacker or a defender?
Michelle
I will be an attacker.
Eddy
Alright, you'll be an attacker, totally fine, your goal Michelle is, using those digits one to nine, we'll take turns, you wanna form a total of 15 somewhere on a row or a column or a diagonal. That's your goal because you chose attacker, I'm the defender, so I'm gonna try and stop you. OK, and the traditional way this game is played is that the defender goes first. So I'm gonna place a number here like say seven.
[He writes the number 7 in the middle-left box.]
Michelle
OK.
Eddy
And remember, your goal is to create a row or column or a diagonal that adds to 15.
Michelle
Yes, OK.
[Michelle uses a green marker to write the number 5 in the middle box.]
Eddy
OK, fantastic. So you put a five there, what I noticed is, if for example, I left this blank...
[He points to the middle-right box.]
Michelle
Yes.
Eddy
..and let you have that move in that spot. Seven plus five gives us 12. So if you had a three available and could put it there, done, game over. I would obviously like to stop you. So I could do a couple of different things, right? I could put some other number that's not three in this box, right, because then you can't put a three there or I could take the three, and I could put it somewhere else because you can only use it once. I'm just gonna go ahead and put a four here because I know it's not a win.
[Eddy places a four in the middle-right box. The entire middle row is now filled with numbers. From left, they are 7, 5 and 4.]
Michelle
I'm already regretting putting the 5 there because now that idea of Iooking for pairs that combine to make ten, I know already that you're gonna chase me down...
Eddy
Sure.
Michelle
..and not permit that to happen. And my only real chance is, might be around the rows not through the diagonal here.
Eddy
Go ahead, put a number anywhere and we'll see how we go.
[Michelle writes an 8 in the top-right box. Eddy points to the bottom right box.]
Eddy
OK, so I know I don't wanna let you have the three there…
[He points to the bottom left box.]
Eddy
…and I also don't want you have the two here. This is starting to become tricky because I now have so many different directions. I've got to think in. I might regret this, but I'm gonna try to put the two there.
[He writes the number 2 in the bottom-right box. The right column is now filled in. From top, the numbers are 8, 4, and 2.]
Michelle
That's what I would have done.
[Michelle points to the 5 and the 2 running on a diagonal line.]
Michelle
Which gives me seven. And I can't get to 15 because I've used eight already.
Eddy
But the game is still very not over. There's still a lot of options.
Michelle
Maybe we could pause.
Eddy
Yeah, here's a great spot. Yeah, that would be the next... yeah, absolutely.
Michelle
What will be your next move so that I can beat Eddy?
Eddy
If you're the attack or the defender, right?
[White text on blue: What are some ways you could make your brain really sweaty?]
Michelle
You might be wondering, what are some ways you could make your brain really sweaty? Let's see a couple of ways we could adapt this game.
[Beside the existing gameboard, Eddy has drawn a second, empty grid. He writes 1 – 9 above the existing gameboard, and then -4 - 4 above the empty gameboard.]
Eddy
There's no reason we have to limit ourselves from one to a nine. You know, there's no reason why we can't say limit them from negative four to four, that's still nine numbers.
[below the -4 – 4, Eddy writes 11 – 19.]
Eddy
Or we could say, well, maybe we go from 11 to 19.
[Eddy writes and then circles the number 15 below where he was written 1 – 9.]
Eddy
And people are then thinking, wait a second, if I play this game, what I'm trying to add up to is 15, which is partly to do with the idea of a magic square and why that adds up nicely. For a game like, say, 11 to 19, 15 is not a good number to add up toward. In fact, it's an impossible number. So what would be a better choice? And there's a whole level of mathematical thinking around, OK, well, how do I re-engineer and adapt this game? So it's delightful how easy it is to extend across a range of students who...
[White text on a blue background: Over to you, mathematicians!]
Michelle
Alright mathematicians, over to you. Have a game of Mathematic-Tac-Toe.
[The NSW Government logo flashes on screen. Text below reads: Copyright, State of New South Wales (Department of Education), 2021.]
[End of transcript]
Instructions
- Decide which player will be the 'attacker' and who will be the 'defender'.
- Players will take turns placing the numbers 1-9 into the grid. Each of these numbers can only be used once.
- The aim of the game is for the 'attacker' to get 3 numbers in a row to add to exactly 15. This can be horizontally, vertically or diagonally.
- However, the aim for the 'defender' is to stop the attacker from getting a total of 15.
- The 'defender' can win once all the numbers have been used and none of the rows, columns or diagonals add to exactly 15.
- Try playing this game with the numbers 11- 19.
Discussion
What would you suggest to be Michelle's next move as the attacker?
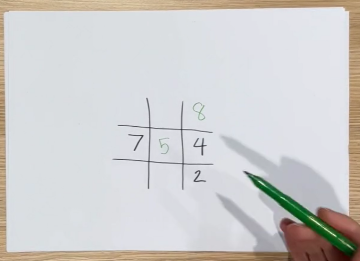
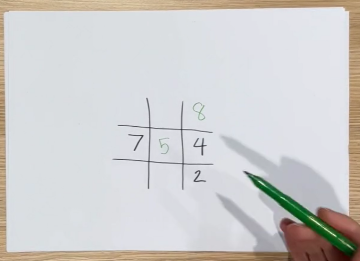
Once you have played the game, what could you do differently next time to increase your chances of winning?
Share/Submit
Share your work with your class on your digital platform. You may like to:
- share your discoveries
- write comments
- share pictures of your work
- comment on the work of others.