Colour in fractions
Stage 3 – A thinking mathematically context for practise focussed on deepening understanding of equivalent fractions
From D. Clarke and A. Roche, Engaging Maths: 25 Favourite Maths Lessons, 2014
Syllabus
Syllabus outcomes and content descriptors from Mathematics K–10 Syllabus © NSW Education Standards Authority (NESA) for and on behalf of the Crown in right of the State of New South Wales, 2023
Outcomes
- MAO-WM-01
- MA2-PF-01
- MAO-WM-01
- MA3-RQF-01
Collect resources
You will need:
- one die labelled 1, 2, 2, 3, 3, 4 in one colour or use a spinner (PDF 584 KB)
another die labelled *2 ,*3 ,*4 ,*6 ,*8 ,*12 in another colour or use a spinner (PDF 584 KB)
coloured pencils or markers.
Watch
Watch the Colour in fractions part 1 video (3:20).
Michelle
[Screen shows 2 Colour in Fractions game boards, a bunch of highlighters, a pen and 2 foam dice. One of the dice has numbers on it, the other has fractions.]
Hello everybody, welcome back to having some fun with mathematics! I'm here again with Ayesha and Barbara. Hi guys!
Ayesha
Hello!
Barbara
Hi Michelle!
Michelle
We're going to play a game today called colour in fractions and sometimes you can play this game by yourself. Sometimes you can play competitively against someone else, and sometimes you can play where is it 2 teams of 2. Today we were limited in our access to mathematicians, so it's Ayesha and Barbara versing me today.
So we have our game board. We've got lots of different markers. We each have a pen and we have our fancy dice which you could also use spinner as well if you don't have these, so, let's play!
Today we're playing a version of the game where we're each going to use the same numbers that roll to see what happens with our game. So what happens is I know this is going to tell me how much and this is going to tell me my unit size.
[Michelle rolls the dice and lands on 2 sixths.]
So what we have here guys is 2 sixths, so now you can form 2 sixths on your board in any way. So you could do something like... we'll,, I'll let you work it out.
Barbara
OK. What do you think Ayesha, should we colour in... these are sixths, should we in 2 of those?
Ayesha
Sounds like a plan!
So what I'm going to record here is what was rolled.
[Barbara highlights 2 sixths on her board whilst Ayesha records what was rolled and what was shaded.]
Barbara
And then we're going to shade 2 sixths. And I’m gonna put that there, so we know what we coloured in.
[Barbara adds an orange dot next to their first row on the gameboard.]
Michelle
[Michelle records her game board and shades 1 third as 2 sixths.]
So you guys had 2 sixths as 2 sixths, and I had 2 sixths as 1 third. And I know they're equivalent 'cause this line down here shows me that 2 sixths is equivalent in value to 1 third. You guys can roll.
Ayesha
[Ayesha rolls the dice and lands on 2 sixths.]
So we have, 2 sixths.
Barbara
So now, what should we do? Should we do what Michelle did last time? Or should we look for another way?
Ayesha
I'm thinking we look for another way.
Barbara
If we do a line straight through, we can either do 1 third... or we can do this one here, which is twelfths. So we could do 4 twelfths.
[Barbara highlights 4 twelfths whilst Ayesha records what was rolled and what was shaded.]
Ayesha
OK.
[No sound. Screen fast forwards to show Michelle, Barbara and Ayesha playing the game.]
Michelle
All right, over to mathematicians to have fun too!
Instructions
- Players take turns to throw both dice or have a spin on their spinners. They make a fraction, the first die or spinner being the numerator. They then colour the equivalent of the fraction shown. For example, if a player rolls a 2 and *4 (or spins 2 and quarters) then they can colour in:
- 2/4 of one line, or
- 4/8 of one line, or
- 1/4 of one line and 2/8 of another, or
- any other combination that is the same as 2/4.
- 2/4 of one line, or
- For each roll or spin, the student should use a different colour pencil or marker.
- If a player is unable to use their turn, they “pass.”
- Players take it in turns to roll or spin and make fractions, marking them on their fraction wall. If the fraction rolled or its equivalence cannot be shaded, they miss a turn. This becomes more frequent later in the game.
- Players are not allowed to break up a “brick.”
- In finishing off the game, the player must have had 18 turns or have filled their wall. A larger fraction is not acceptable to finish.
The first player who colours in their whole wall is the winner, but the other player is encouraged to keep going (with the support of the first player) to fill their fraction wall, or the greatest number of wholes. If after 18 turns neither player colours in their whole wall, the player with the greatest number or wholes wins!
Discussion
If you played the game tomorrow, what would you do differently?
If you were giving some hints to a younger brother or sister who was about to play the game, what would you say to him or her to help them win?
Reflection
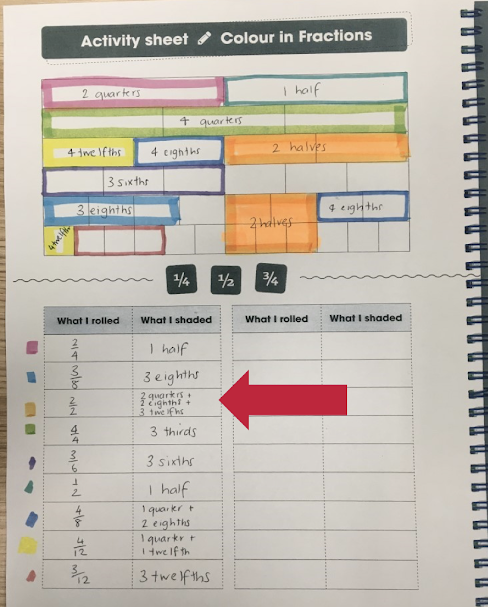
We noticed something when we played, Michelle recorded 2-halves (2/2) as being equivalent in value to 2 quarters+ 2 eighths + 3 twelfths (2/4 + 2/8 + 3/12).

Watch
Watch the Colour in fractions part 2 video (1:43).
Michelle
Hi everybody! We wanted to come back and explore this idea in our colouring fractions game of 2 halves being equivalent to 2 quarters, 2 eighths and 3 twelfths as we can see here.
So we wanted to show you a strategy that you can use to help prove that this is an accurate way of describing or renaming 2 halves. And so to help me do that, I've taken a copy of my game board and I have a pair of scissors and I'm just going to cut those sections out.
[Michelle cuts each of the sections from her gameboard out.]
Excellent! And so now what I have is part of what I said was 2 halves and the other part of what I said was 2 halves and I actually have inside of this 2 quarters, my 2 eighths and 3 of my twelfths. And if I take them and lay them over the top of the halves line I can see that 2 quarters is the same as one half and if I join 3 twelfths with 2 eighths, that also turns out to be equivalent to another half, and so that's how I can say 2 quarters and 2 eighths and 3 twelfths is the same as 2 halves, or in fact, how I can prove it.
Now what we're wondering is how many different ways could you make 2 halves?
Over to you!
Instructions
What is something interesting that you discovered when exploring equivalent fractions today?
Discussion
You may like to play Colour in fractions again and investigate equivalent fractions again on this gameboard.
Now, explore your own game board to investigate equivalent fractions. What equivalent fractions can you investigate using your gameboard?
How many other ways can you find to rename Michelle's chosen section of 2-halves?
Share/Submit
Share your work with your class on your digital platform. You may like to:
- share your discoveries
- write comments
- share pictures of your work
- comment on the work of others.