Understanding units of measurement
What is understanding units of measurement?
Understanding units of measurement encompasses how a student becomes increasingly able to recognise attributes that can be measured and how units of measure are used and calculated. Transitioning from informal to formal units, a student attends to the structure of the unit used to measure. The structure of the units gives rise to ways of calculating length, area and volume.
The National Numeracy Learning Progression element of Measurement and geometry is where we locate the sub-element of Understanding units of measurement. This sub-element helps teachers to develop fine-grain understanding of student numeracy development in measurement, by guiding teachers to support students whose development is above or below stage equivalents in syllabuses.
Understanding units of measurement describes how students: are able to recognise attributes that can be measured; use and calculate with units of measure; make the transition from informal to formal units; develop the structure of units allowing them to calculate length, area and volume; and deal with mass and capacity, using personal referents and estimation skills.
The relationship between units of measurement is commonly applied in decimals, ratio, rates, percentages and proportions found in the sub-elements of: Number and place value (NVP); Multiplicative strategies (MuS) and Proportional thinking (PrT).
As Professor Dianne Siemon suggests in her book Teaching Mathematics:
“Making meaningful measurements and estimating measurements both depend upon a personal fluency with the unit of measurement being used,” and, “Measuring skills are essential to successful numerate behaviour in managing day-to-day situations.”
Understanding units of measurement is a sub element within Measurement and geometry element of the National Numeracy Learning Progression (NNLP).
Within the sub-elements of the numeracy progression, subheadings have been included to group indicators into particular categories of skills that develop over a number of levels. The subheadings within the Understanding units of measurement sub-element are:
- Describing the size of objects (UuM1)
- Comparing and ordering objects (UuM2)
- Using informal units of measurement, Estimating measurements (UuM3)
- Repeating a single informal unit to measure, Estimating measurements , Describing turns (UuM4)
- Using abstract units, Angles as measures of turn (UuM5)
- Using formal units, Angles as measures of turn (UuM6)
- Using formal units and formulas, Angles as measures of turn (UuM7)
- Converting units, Using formal units and formulas, Angles as measures of turn (UuM8)
- Using formal units and formulas, Circle measurements (UuM9)
- Using formal units and formulas, (UuM10)
The following video explains the links between mathematics and numeracy.
It is important that we establish not only the links between mathematics and other key learning areas, but also the link between mathematics and numeracy, as these are the connections that create meaningful contexts for extended learning. If we want our students to use their mathematical knowledge ‘in action’ across the curriculum and in everyday life, then it’s important that they have not only the knowledge and skills to do this, but also the confidence to do it.
Maura Sellars explains, students do not automatically learn numeracy skills in mathematics times in classrooms, they need to have multiple opportunities to develop competencies in numeracy by solving real problems. Making explicit linkages and connections and discovering and exploring number and other conceptual relationships helps students to develop robust knowledge that is easily transferred from familiar to unfamiliar contexts and problems. Numeracy, like literacy, is fundamental to students’ capacities to make meaning of their world.
Dianne Siemon believes measuring skills are essential to successful numerate behaviour in managing day-to-day situations.
Bishop (1988) identified 6 fundamental activities that occur across all cultures, one of these was ‘measuring’ which he describes as quantifying qualities for the purposes of comparison and ordering, using objects or tokens as measuring devices with associated units or ‘measure-words’.
Reference: Bishop. A. J. (1988) Mathematical Enculturation: A cultural perspective on mathematics education. Department of Education, University of Cambridge.
The relationship between units of measurement is applied in ratios, rates and proportions as well as decimals and percentages.
Follow Juliana as she measures a garden path and converts the measurement from metres to centimetres in the garden path video.
Juliana would like to have a pathway from her back door to the garden shed. She measures the distance to be 5376 millimetres long. Juliana needs to convert this measurement into metres to purchase an accurate number of pavers for her path.
Let’s consider the steps needed to convert 5376 millimetres into metres. Using a number line and a conversion chart may help Juliana with her calculations.
To convert 5376 millimetres into metres, she must: First, divide by 10 to get to centimetres, then divide by 100 to get to metres. Meaning, 5376 millimetres is equivalent to 5.376 metres.
So where is 5.376 on a number line?
5.376 is between 5 and 6. By zooming in, she can see there are 10 divisions between 5.0 and 6.0.
When she considers 5.376, she knows it is bigger than 5.3, but less than 5.4. 5.376 is between 5.3 and 5.4. By zooming in she can see there are 10 divisions between 5.30 and 5.40.
This means there are 100 divisions between 5 and 6.
When she considers 5.376, she knows it is bigger than 5.37, but less than 5.38. 5.376 is between 5.37 and 5.38. By zooming in she can see there are 10 divisions between 5.370 and 5.380. This means there are 1000 divisions between 5 and 6. She can find the exact position of 5.376 when she divides 5 and 6 up into thousandths.
By zooming out again, she can see where 5.376 is on the number line. By understanding units of length and having a knowledge of decimals, Juliana is able to convert her measurement of 5376 millimetres into 5.376 metres and accurately complete the paving of her garden path.
Language of measurement
Even though numeracy and mathematics are symbolic in nature, oral and written languages need to be used to support and enrich it. The language of measurement is pivotal in the development of skills and attributes.
Students should be able to communicate using the following language:
Formal units: millimetre, centimetre, metre, kilometre, square unit, cubic unit, millilitre, litre, kilolitre, milligram, gram, kilogram, tonne
Length: distance, perimeter, dimension, measure, end-to-end, side-by-side, tall, taller, short, shortest, longer than, wide, across, diameter, radius
Area: width/wide, breadth, square units, perpendicular height, respectively, two-dimensional, surface area, sector, segment, composite
Volume and capacity: cubic unit, three-dimensional, prism, pyramid, cylinder, sphere
Mass: weight, weigh, heavy, heavier, lighter, pan balance, level balance, gross, net
Equipment: rulers, tape measures, scales, containers- cups
Some students often confuse concepts such as big, tall, long and high. Engage students in activities that help them differentiate between these concepts.


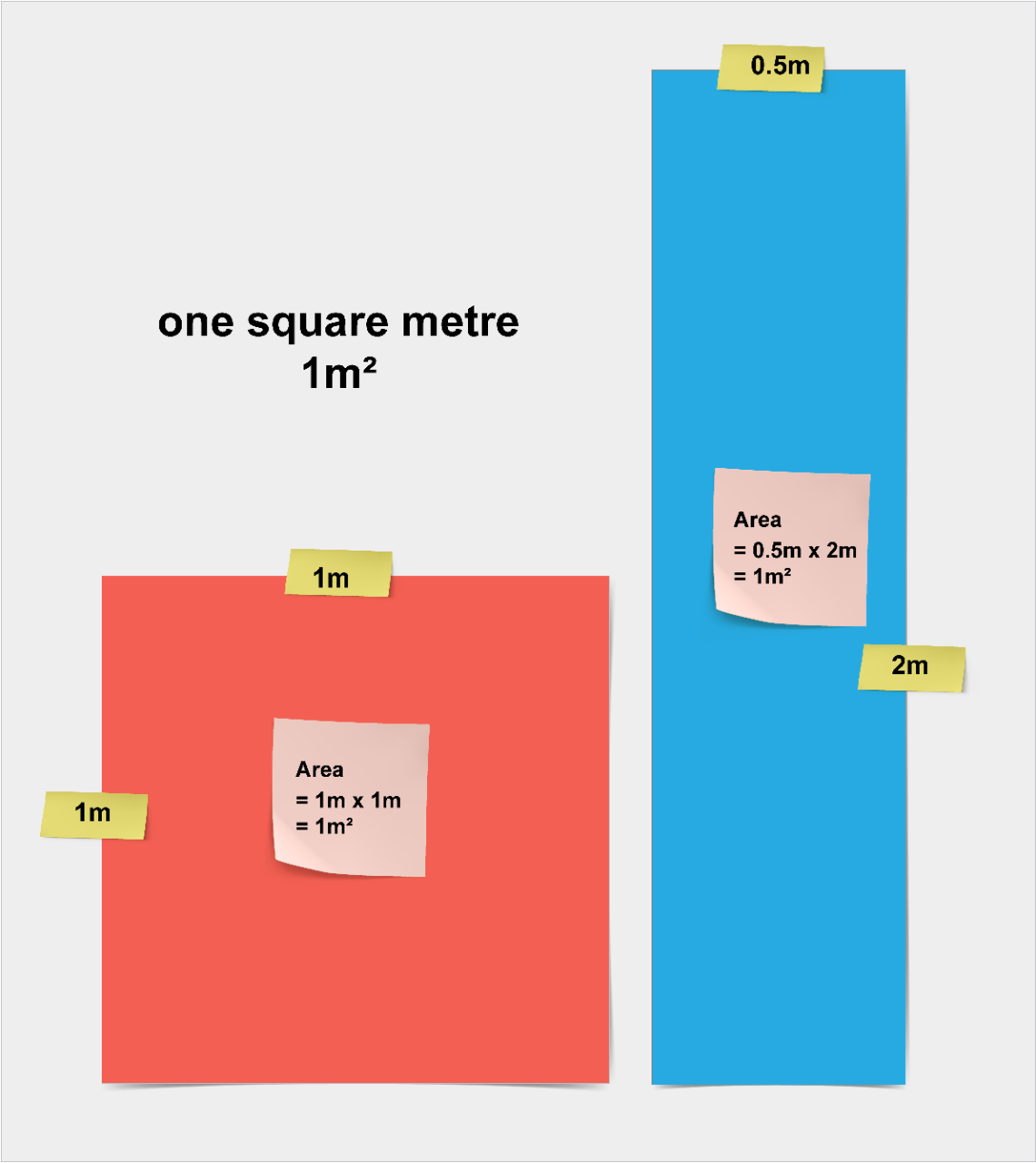
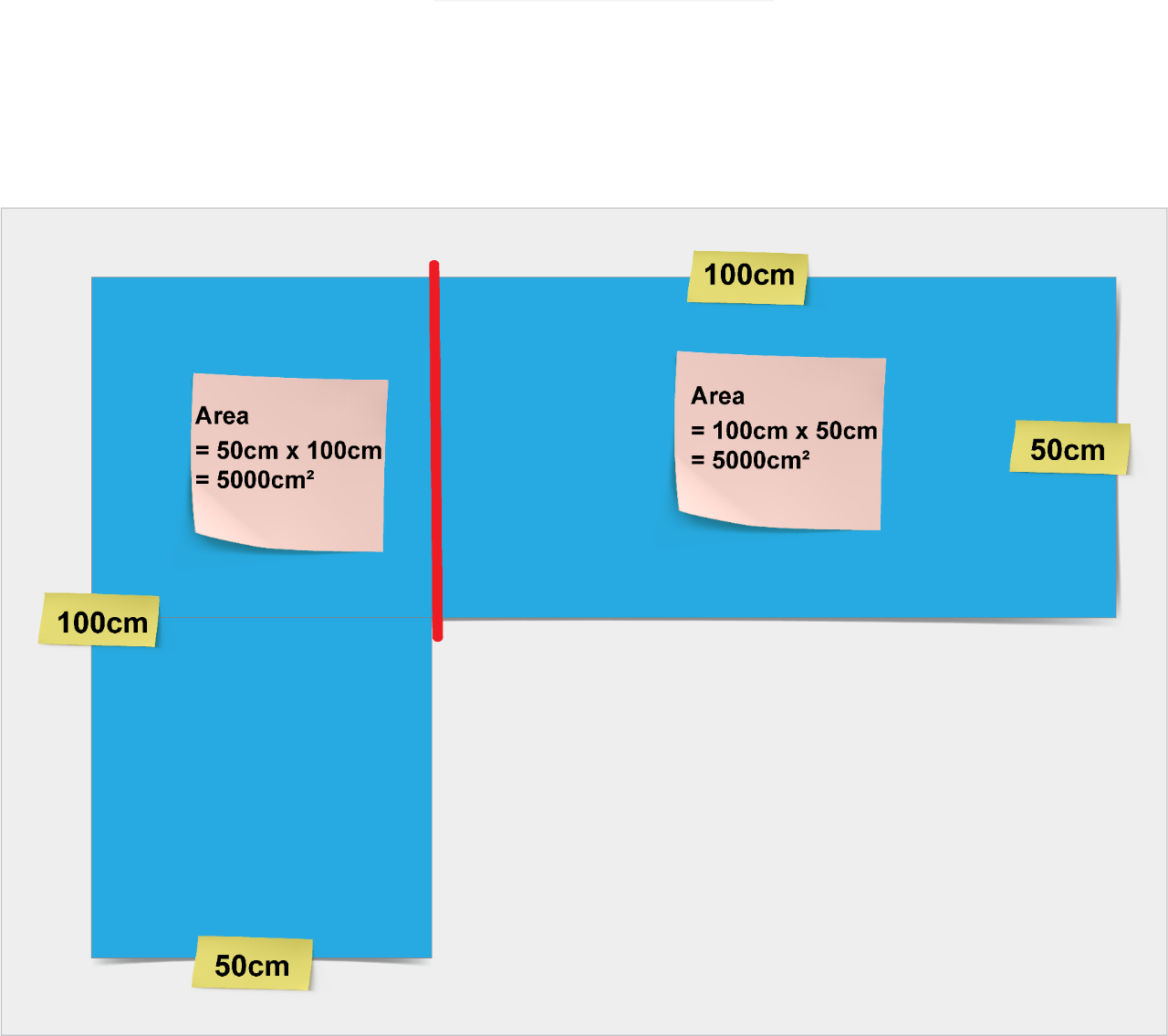
What does one square metre look like?
The abbreviation m2 is read as 'square metre(s)' and not 'metre(s) squared' or 'metre(s) square'.
When units are not provided in an area question, students should record the area in 'square units'.

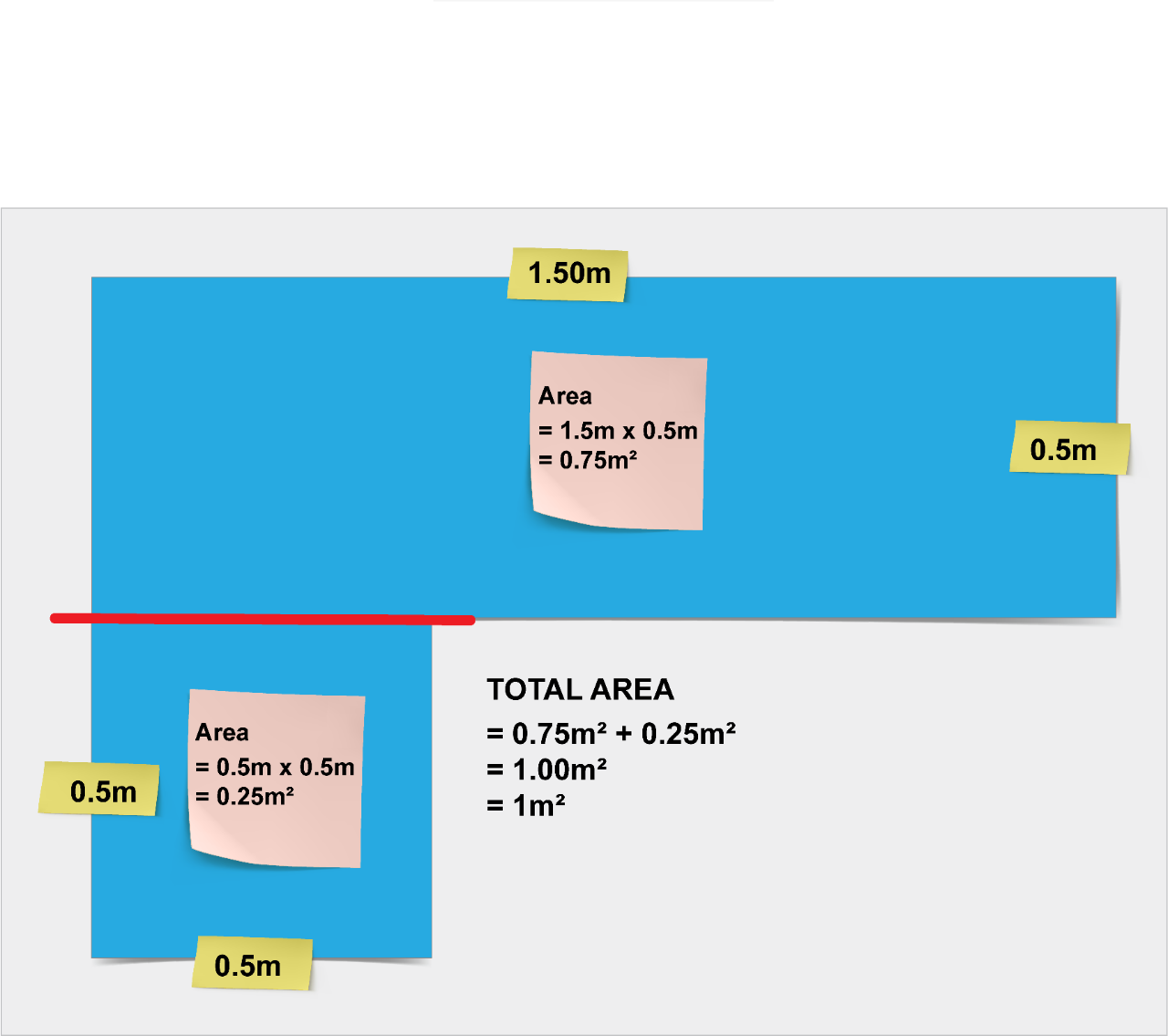

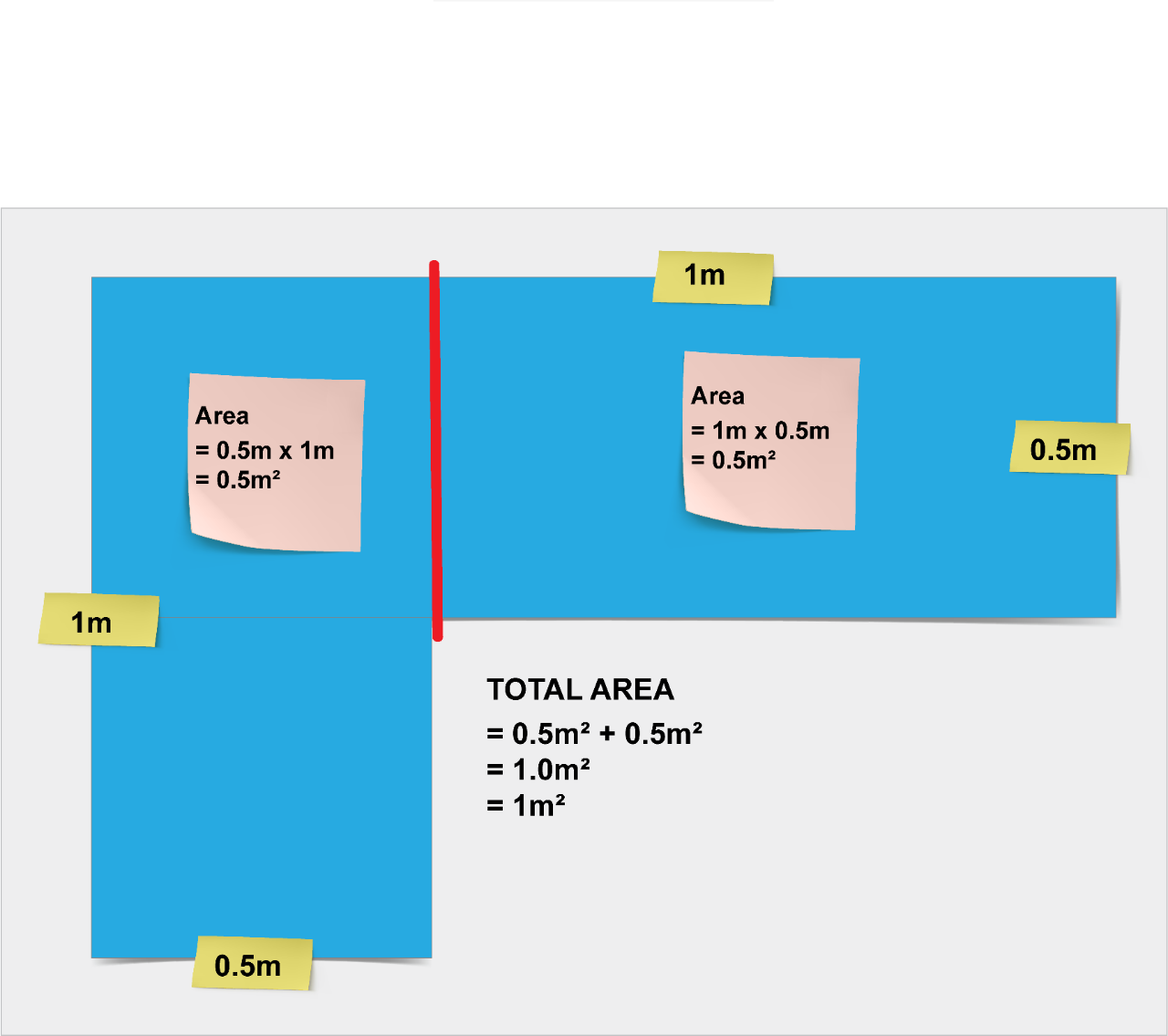

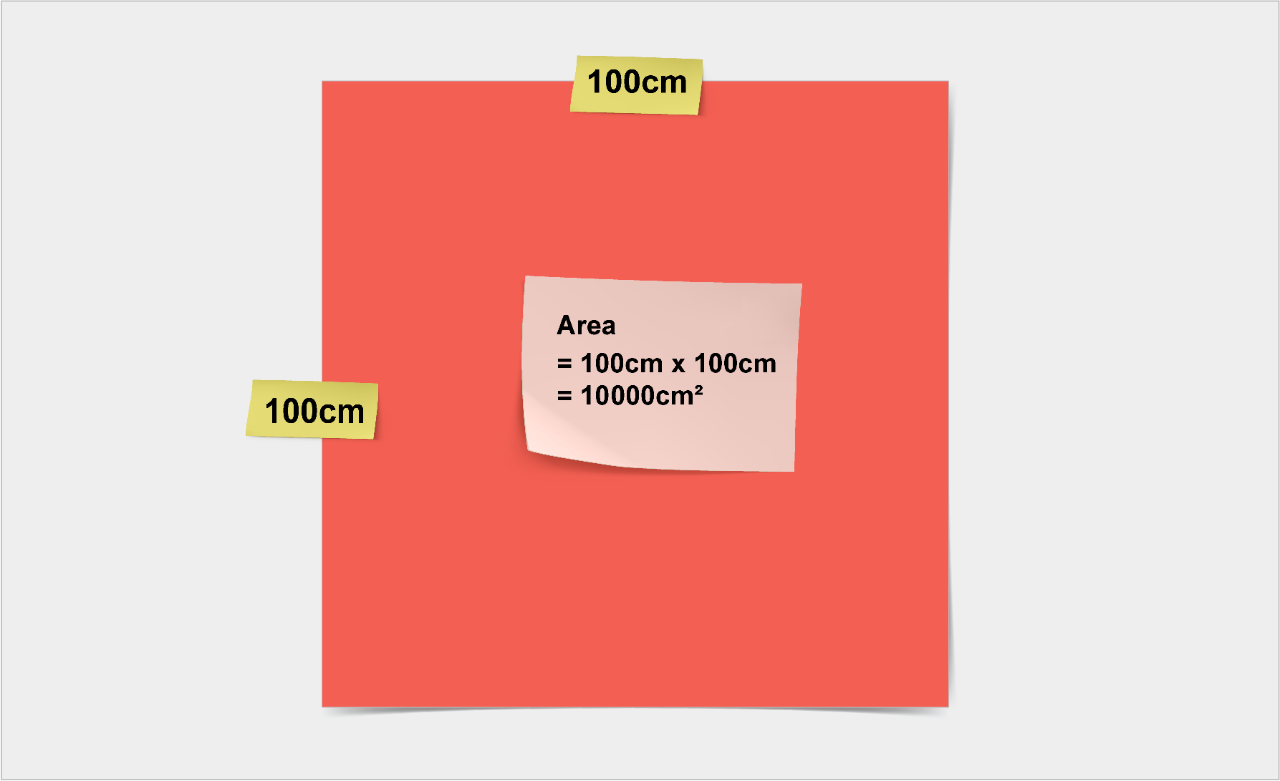
How many cm2 in a square metre?


Classroom resources
- Teaching strategies for teaching measurement
- A teaching resource to support students in achieving the HSC minimum standard in numeracy (staff only)
- Numeracy resources in Universal Resources Hub (staff only) - (search ‘measurement’)
