Multiplicative strategies
What are multiplicative strategies?
Multiplicative strategies encompass a student’s ability to manipulate numbers in multiplicative situations. Students’ understanding of numbers as composite units and the ability to recognise and work with the relationship between quantities is a critical part of thinking multiplicatively. Students need to understand the relationship between division and multiplication and develop the ability to flexibly use these as inverse operations when solving problems.
Professor Dianne Siemon describes multiplicative thinking as:
- a capacity to work flexibly and efficiently with an extended range of numbers (that is, larger whole numbers, decimals, common fractions, ratio and per cent),
- an ability to recognise and solve a range of problems involving multiplication or division including direct and indirect proportion, and
- the means to communicate this effectively in a variety of ways (for example, words, diagrams, symbolic expressions, and written algorithms).
Multiplicative strategies is a sub-element within the Number sense and algebra element of the National Numeracy Learning Progression.
Within the sub-elements of the numeracy progression, subheadings have been included to group indicators into particular categories of skills that develop over a number of levels. The 7 subheadings within the Multiplicative strategies sub-element are:
- Forming equal groups (MuS1)
- Perceptual multiples (MuS2)
- Figurative (imagined units) (MuS3)
- Repeated abstract composite units (MuS4)
- Coordinating composite units (MuS5)
- Flexible strategies for multiplication/ Flexible strategies for division (MuS6)
- Flexible number properties (MuS7)
Flexible strategies for multiplication
Number sense forms the foundation of all mathematical work. Having a ‘feel’ for numbers and understanding how to work flexibly and creatively with them is not just the domain of single units. In fact, being able to think flexibly about composite units is critical to all mental strategies for multiplication and division, laying the foundations for later mathematical concepts. Building strong number sense requires an understanding of numerical relationships, the use of strong mental imagery and the active making of connections between representations, situations, concepts, experiences and language.
(Adapted from Siemon, D., Beswick, K., Brady, K., Clark, J., Faragher, R., & Warren, E. (2015). Teaching mathematics. South Melbourne, Vic.: Oxford University Press.)
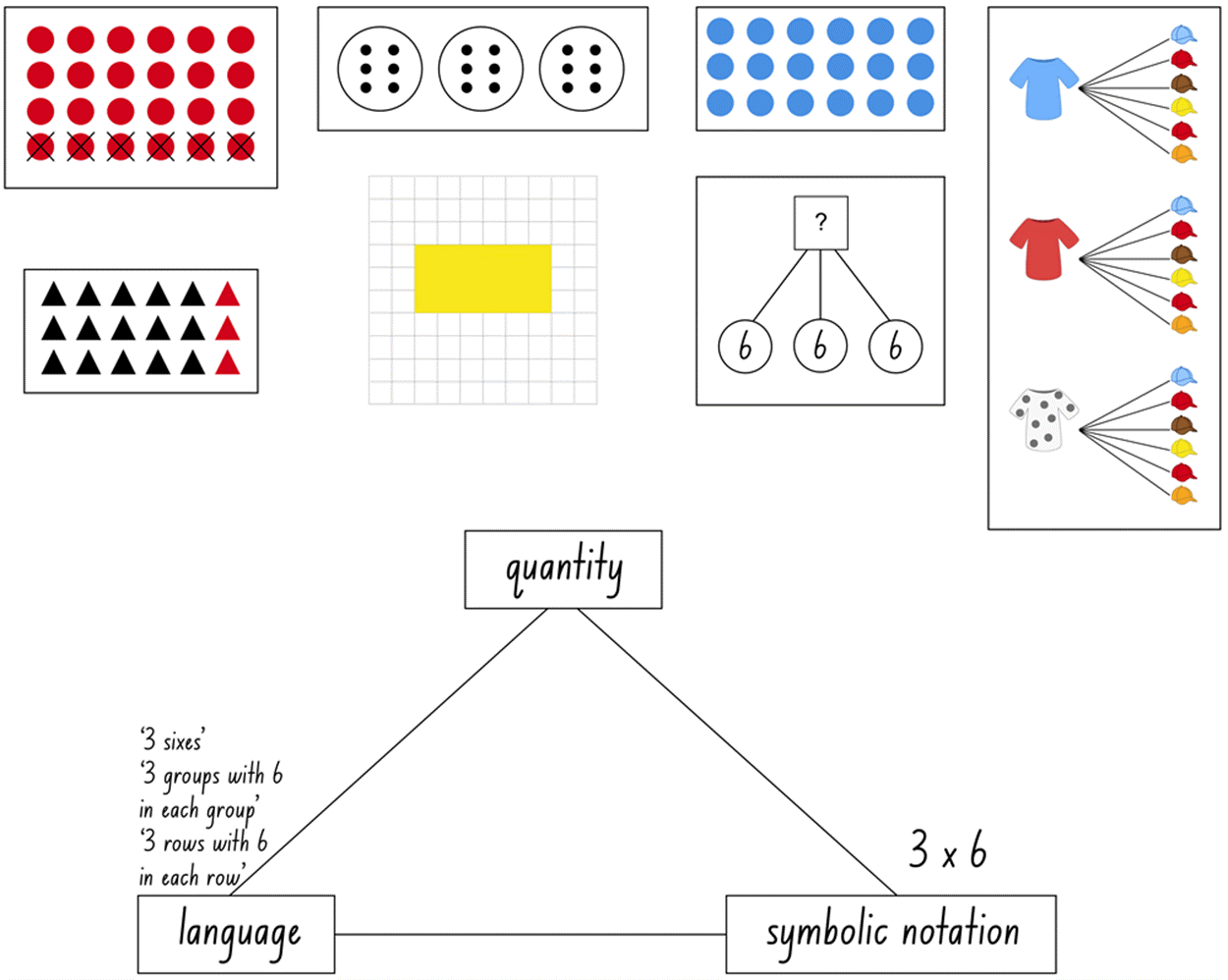
What are you noticing?
The following classroom illustrations demonstrate flexible use of multiplicative strategies.
Moving from concrete to abstract representations
The following video explores the importance of navigating carefully from concrete to abstract representations of multiplicative situations to ensure students gain conceptual understanding (Stage 2).
To develop conceptual understanding in students, we explicitly need to make the connection between concrete, visual, and symbolic representations of multiplicative thinking.
Let us consider seven eights as an array and how this visual representation can support the development of a deeper and more flexible understanding in multiplicative processes and symbolic representations. Students require support as they experience a broad range of mathematical models and when introducing the multiplication symbol as it is a formal mathematical representation. Clear links are needed to demonstrate how concrete and visual representations transition to the symbolic.
Professor Diane Siemen's representation of the multiplication grid supports students as they transition to abstract representations.
This model continues to provide a concrete reminder as students unpack multiplication, and make links to prior learning.
Time is required to support students' conceptual understanding, to appreciate the complexities involved in multiplicative thinking, and the connections between the representations.
The role of talk
Kazemi and Hintz (2014) outline 4 key principles for classroom discussions about strategies. These principles are:
- Discussions should achieve a mathematical goal
- Students need to know what and how to share
- Teachers need to orient students to one another and the mathematical ideas to achieve the mathematical goal
- Teachers must communicate that all students are sense makers and that their ideas are valued.
They also highlight several targeted discussion routines that create productive discourse in the classroom.
The following video provides an explanation and example of the targeted discussion routine.
Troubleshoot and revise is a targeted discussion to help students reason through which strategies produce a correct solution or to figure out strategies that went awry. By sharing their strategies, students can review and revise their thinking or adapt a new strategy from a peer. The goal of this troubleshoot and revise targeted discussion is to explore why a particular mathematical strategy didn't work.
Focusing on the links between concepts and representations (···1.2s) after an open strategy sharing using the problem 25 by 18, A student asked for some clarification about why their answer was different
I did 25 times 20 to get 500, and then I subtracted two to get 498.
I think it should work because 20 is just two more than 18, but I'm not sure why I'm not getting the same answer as other people when I think I should be.
Jesse has an efficient strategy by rounding 18 to 20.
They use benchmark numbers to make the problem more efficient. It might help us to put these numbers into a story to work out why Jesse is getting a different answer.
Let's imagine Jesse had 25 packets of coloured pencils with 18 pencils in each packet.
I'm now going to add another two pencils to each packet to represent how Jesse used the benchmark number of 20Oh, I see.
When Jesse changed the numbers to 25 times 20, it looked like there were 25 packets with 20 pencils in each packet, but he needs to remember that there are only 18 pencils in each packet, and he has increased the number in each of the 25 packets and not just in one packet. The teacher can now use the strategies of wait time and turn and talk so students can consider the question how many pencils need to be removed from each packet?
By troubleshooting Jessie's thinking, we can revise their strategy and identified that we needed to subtract 25 groups of two instead of one group or two. This number sentence shows the strategy used 25 by 18 is equal to 25 by 20 minus 50.
Jesse, can you explain your revised thinking?
When I subtracted 2 from the 500, I only subtracted one group of 2. That's why I got 498. I should have subtracted 25 groups of two, which is 50. Now I get the answer of 450.
Resources
- The 4-part flexible strategies resource supports flexible multiplicative thinking. Use this series to support a connected network of critical mathematical concepts, skills and understanding.
- Teaching strategies include a range of engaging interactive activities for Stage 1 to Stage 5 to support the development of skills in multiplication and division.
- The Mathematics digital student resource - thinking mathematically K-6 site provides valuable resources including tasks, rich games and investigations.
- Representing multiplicative situations using arrays
- Representing the numbers 1-20 multiplicatively
- Talk moves
- Think board template (PDF 103KB)
- Planning for questioning (PDF 108KB)
- Student feedback - challenge and enjoyment template (PDF 144KB)
Reference
Kazemi, E., & Hintz, A. (2014). Intentional Talk – How to structure and lead productive mathematical discussions. USA: Stenhouse Publishers.