This resource has been developed in partnership with the NSW Mathematics Strategy Professional Learning team, Curriculum Early Years and Primary Learners, and Literacy and Numeracy.

About patterns

Patterns are at the heart of mathematics. All patterns have regularities that we can perceive visually, auditorily and somatically (through tactile or action-based sensations). To discern, describe, extend, adjust, make and translate patterns, we need to be able to identify the repeating core, or pattern unit.

The image below shows a row of blocks that alternate in colour: blue-red-yellow-blue-red-yellow-blue-red-yellow:

The use of the same three coloured blocks, arranged in a particular order, over and over and over again, creates a repeating pattern. This is a three-part pattern as it has three parts that make up the pattern core (in this instance, a blue block, a red block and a yellow block).

To be able to clearly describe this pattern with further precision, we need to have language to describe the composition of the 3-parts of the pattern core.

A pattern with a 3 parts repeating core where each part has a unique attribute is described as an ABC pattern. In the example above, the core has 3 parts and each part has an unique attribute (changing colour):

An ABB has pattern has 3 parts with two unique attributes, one of which is repeated. In the example below, there is a blue block, followed by a repeating red block:

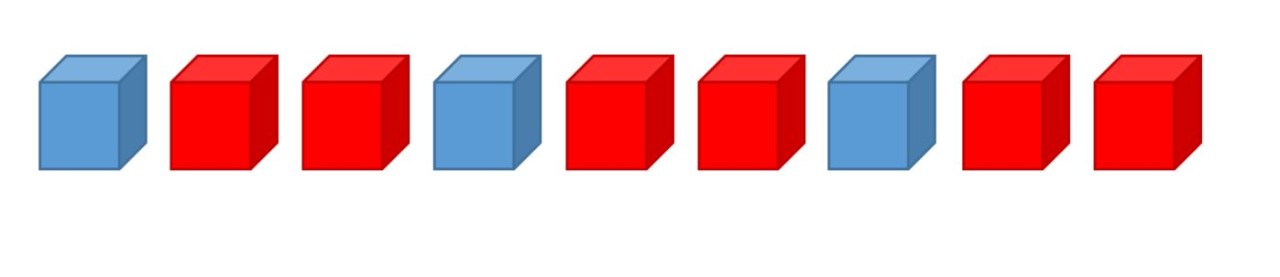
An ABA pattern also has a core of 3 parts with two unique attributes, one of which is repeated. In the example below, the blue block is used before and after the red block:

To know that we have detected a pattern, we have to see the repeated core, or pattern unit, repeat. If we only see blue-red-yellow (ABC), we don’t have enough evidence to know we have a pattern. If we see the ABC unit repeating, as in blue-red-yellow-blue-red-yellow-blue-red-yellow, then we can be confident of our judgment that a pattern, a mathematical regularity, is present. Typically, we like to see something happen over and over and over in order to feel confident a pattern is present.

Patterns come in different forms. For example, we can find:

• Repeating patterns (described above)
• Growing and shrinking patterns (such as the patterns we find in the backward counting sequence where each number is one less than the number before)
• Structural/spatial/visual patterns
• Combinatorial/computational patterns

Patterning can also include exploring mathematical structures and leads into algebraic thinking. Algebraic thinking, like patterning, is foundational to mathematical thinking as it provides the language and structure to represent ideas, solve problems, model situations and prove generalisations. When we describe a 3-part pattern as ABC we are supporting students to make connections between patterns and algebra.

The Becoming mathematicians: Exploring patterns professional learning video and accompanying resource examines some components of exploring patterns, from Kindergarten to high school.

Access 'Becoming mathematicians: Exploring patterns' via MyPL (course code NR29611.).

Supporting tasks

Full instructions on how to use each of these tasks, including materials, related tasks and learning intentions are included in the resource, available for download on this page.

Sorting

Sorting and classifying tasks help students to develop a range of thinking skills and build the foundations for reasoning, communicating and problem-solving. Being able to notice various attributes within the same collection also promotes flexibility and creativity in thinking – critical aspects of mathematics and mathematical thinking.

Task 1: Sorting 1

Students watch the ‘Sorting 1’ video to learn how to play. then draw pictures of the different ways they organised items.

Exploring patterns

To identify a pattern, we need to see the core repeated over and over and over again (about three times to be able to trust that we have found a regularity). The repeating core of a pattern can be described using letters to support moving from the specific to being more generalisable.

Task 2: Exploring patterns 1 and 2

Students watch ‘exploring patterns’ (videos 1 and 2) and create patterns with missing parts and AB patterns.

Task 3: Exploring pattern 3

Students watch exploring patterns (video 3) then build on their patterns developed in task 2, changing shape, size, position and quantity.

Task 4: Dice patterns A and B

Students watch dice pattern videos A (investigation 1–4) and B (investigation 5–6), then play memory using matching cards

• Variation: Play other matching games such as ‘go fish’ with the cards.

Staircase patterns

Task 5

Students watch the Numberblocks Step Squad episode, followed by the ‘staircase pattern’ videos (parts 1 and 2) then draw and investigate staircase patterns.

• Variation: Continue with the ‘staircase pattern – follow up’ videos (parts 3 and 4)